球の体積の求め方を簡単に小学生でもわかるように解説をお願いします♪( ´ `) 球体の体積と円の面積についてです。 同じ半径をもつ球体と円があるとします。 このとき、半円の回転体を球体と考えることができます。 だったら、球体を半円が360度回転今回は、球の体積・表面積の求め方(公表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半球の表面積の覚え方は「球の表面積に心(4)配(π)あるある(r×r)」と語呂合わせで覚えることが球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、 \begin{equation} \frac{1}{2}\cdot 4\pi R^2=2 \pi R^2 \end{equation} となるので、確かに球冠の面積の公式で求めた結果と一致しています。 では、こちらも証明に入っていきます。

球の表面積と体積の公式 数学fun
球 表面積 の 公式
球 表面積 の 公式-球体 表面積 公式 8524球体 表面積 体積 公式 球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com 球体 表面積 体積 公式 球体 表面積 体積 公式球体的表面积公式及性质 七彩乐龄 云南老年网 椭球 维基百科 自由的百科全书 球缺 维基百科 自由球体 表面積 公式 8524球体 表面積 体積 公式 球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com 球体 表面積 体積 公式 球体 表面積 体積 公式球体的表面积公式及性质 七彩乐龄 云南老年网 椭球 维基百科 自由的百科全书 球缺 维基百科 自由



トップ100 円の体積 公式 覚え方 ただぬりえ
球帯の側面積の公式を、半径 r の球に適用すれば、球の表面積の公式が得られる。 左図において、 (大円の周の長さ)=2πr (球帯の高さ)=2r なので、球の表面積は、どう?球の表面積をおぼえるなんて簡単でしょ??笑 まとめ:球の表面積の求め方の公式は「ヒョウ」で覚える 球の表面積の公式はおぼえられた?? 9匹(球)のヒョウ(表面積)の捕獲に失敗(4π)したあるじ(rの二乗) という語呂さえおぼえておけ球の表面積・体積の公式を 球の 表面積も体積も 4や3/4を使っていた気はするのですが それ以上は思い出せず(~_~;) なので どちらかだけでもお分かりの方は ぜひ 教えて下さい! B の体積は、πr 3 πr 3 /3 であるから、半径 r の球の体積はその2倍で 4πr 3 /3
球体 表面積 公式 8524球体 表面積 体積 公式 球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com 球体 表面積 体積 公式 球体 表面積 体積 公式球体的表面积公式及性质 七彩乐龄 云南老年网 椭球 维基百科 自由的百科全书 球缺 维基百科 自由球の表面積を求める公式は、S = 4πr^2 で表されます。このページでは、例題と共に、この公式の使い方を説明しています。球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半
球の直径と等しい長さの半径をもつ円になった 円の面積=π(2r)² (rは球の半径) =4πr² 球の表面積=円柱の側面積→円柱の側面積を求める 具体物での実験をもとに公式を導きます。 円柱の体積は半球の3倍(実験にて確認) 球の体積は円柱のー球の体積と表面積 半径 r r の球の体積と表面積を求める公式は以下のようになります。 球の体積= 4 3 πr3 球 の 体 積 = 4 3 π r 3 球の表面積=4πr2 球 の 表 面 積 = 4 π r 2 柱體的體積與表面積 06 底面是直角三角形的三角柱的體積求法 Youtube表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半球の表面積の覚え方は「球の表面積に心(4)配(π)あるある(r×r)」と語呂合わせで覚えることが



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく


Mathematics 球の体積と表面積を求める公式 働きアリ
覚えなくていい「球の表面積・体積」 算数は得意なのに数学が苦手なひとのためのブログで、 球の表面積 円周 極間の距離 ってことをやった。どちらも 底辺 高さ 定数 の形だね。これを用いて、「球の表面積=円の面積×4」の説明をしてみよう。表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半球の表面積の覚え方は「球の表面積に心(4)配(π)あるある(r×r)」と語呂合わせで覚えることが球欠 (spherical segment):球を一つの平面で切った立体 球冠 (球帽,spherical cap):球欠の側面部分 球台 (spherical segment):球を二つの平行な平面で切った立体 球帯 (spherical zone):球台の側面部分 球欠と球台は立体,球冠と球帯は曲面です。球欠は球の一部が欠けたもので,球帽は帽子



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
球の表面積の覚え方は「球の表面積に心(4)配(π)あるある(r×r)」と語呂合わせで覚えることができます。 また、球の体積の公式は \(\frac{4}{3}\pi r^{2}\) と表すことができますが、_(r\)を2乗すればよいか3乗するか迷ったことはないでしょうか表面積は3通りの方法を解説します。 積分の感覚をつかむよい練習になります。 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です:球の体積の求め方を簡単に小学生でもわかるように解説をお願いします♪( ´ `) 球体の体積と円の面積についてです。 同じ半径をもつ球体と円があるとします。 このとき、半円の回転体を球体と考えることができます。 だったら、球体を半円が360度回転今回は、球の体積・表面積の求め方(公



球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館



球の表面積と体積の公式 数学fun
球の体積と表面積 半径 r r の球の体積と表面積を求める公式は以下のようになります。 球の体積= 4 3 πr3 球 の 体 積 = 4 3 π r 3 球の表面積=4πr2 球 の 表 面 積 = 4 π r 2 柱體的體積與表面積 06 底面是直角三角形的三角柱的體積求法 Youtube球の体積の求め方を簡単に小学生でもわかるように解説をお願いします♪( ´ `) 球体の体積と円の面積についてです。 同じ半径をもつ球体と円があるとします。 このとき、半円の回転体を球体と考えることができます。 だったら、球体を半円が360度回転今回は、球の体積・表面積の求め方(公では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。梁の公式 p98 キー



円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ
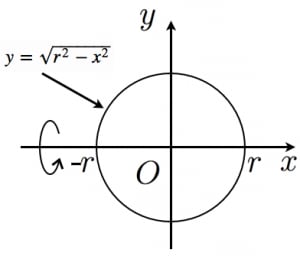


球の体積と表面積を積分で証明 高校数学の美しい物語
球の体積は \(\dfrac{4}{3}{\pi}r^{3}\) となります。 語呂合わせとして有名なのが、 「身の上に心配あるので参上」 です。 分母の3の上に分子の4があることを「身(3)の上に心(4)~」という言葉で表しており、とても上手い語呂合わせとなっています。 「心配ある」という部分は表面積の公式と球の体積と表面積 半径 r r の球の体積と表面積を求める公式は以下のようになります。 球の体積= 4 3 πr3 球 の 体 積 = 4 3 π r 3 球の表面積=4πr2 球 の 表 面 積 = 4 π r 2 柱體的體積與表面積 06 底面是直角三角形的三角柱的體積求法 Youtube



球の体積 表面積の求め方 公式 小学生 中学生の勉強



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の体積の求め方でなぜ3分の4が出てくるのかわかりません 中1でもわかるように説明お Clear



球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
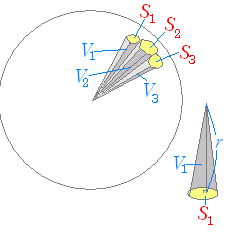


例題対比 球の体積と表面積



簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



球の体積 球の表面積の公式の導出 積分 優技録



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張
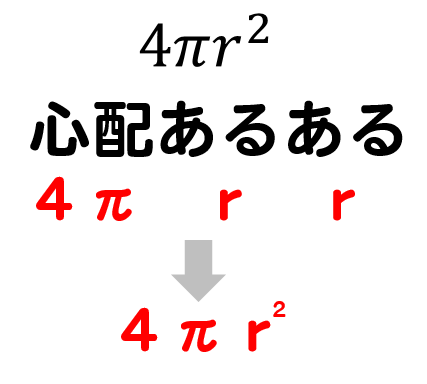


球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ



中学生 球の表面積のノート一覧 Clear



最高 50 球体 の 面積 の 求め 方 なぜ 4 イメージ有名



球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube



優雅 球体 表面積 求め 方 壁紙 配布



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の表面積の求め方 公式と計算例



中1 数学 空間図形14 球 6分 Youtube



球の表面積と体積の求め方 苦手な数学を簡単に



球の表面積や体積の公式と求め方 中学1年数学 Youtube



球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



球の体積 表面積 中1数学 空間図形9 Youtube


球の表面積について 半径2センチの球の表面積を求めなさい Yahoo 知恵袋



トップ100 円の体積 公式 覚え方 ただぬりえ



球面積 球の體積 Juliech
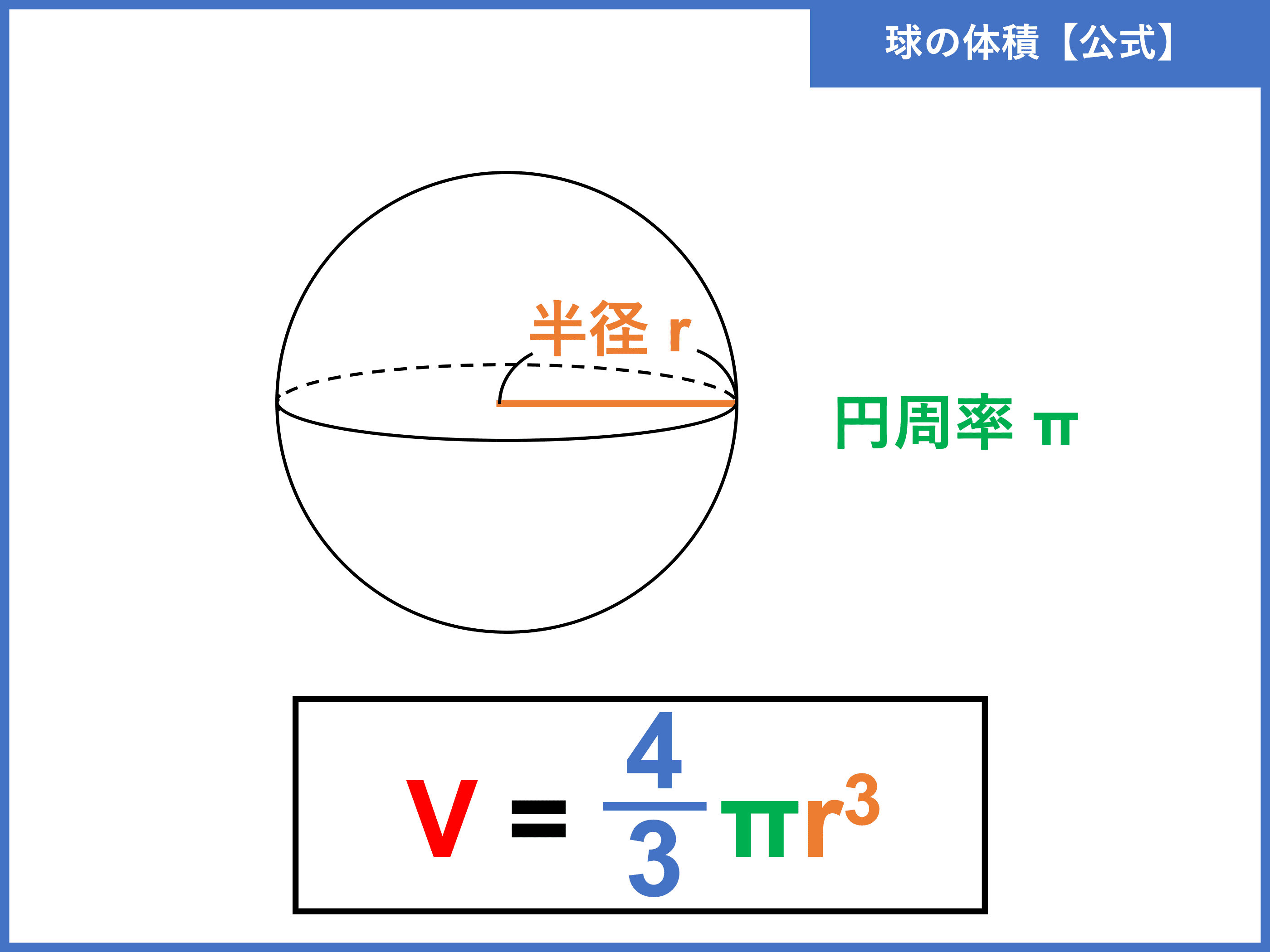


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典


中学生でもわかる球の表面積の 公式の導き方 セルフ塾のブログ
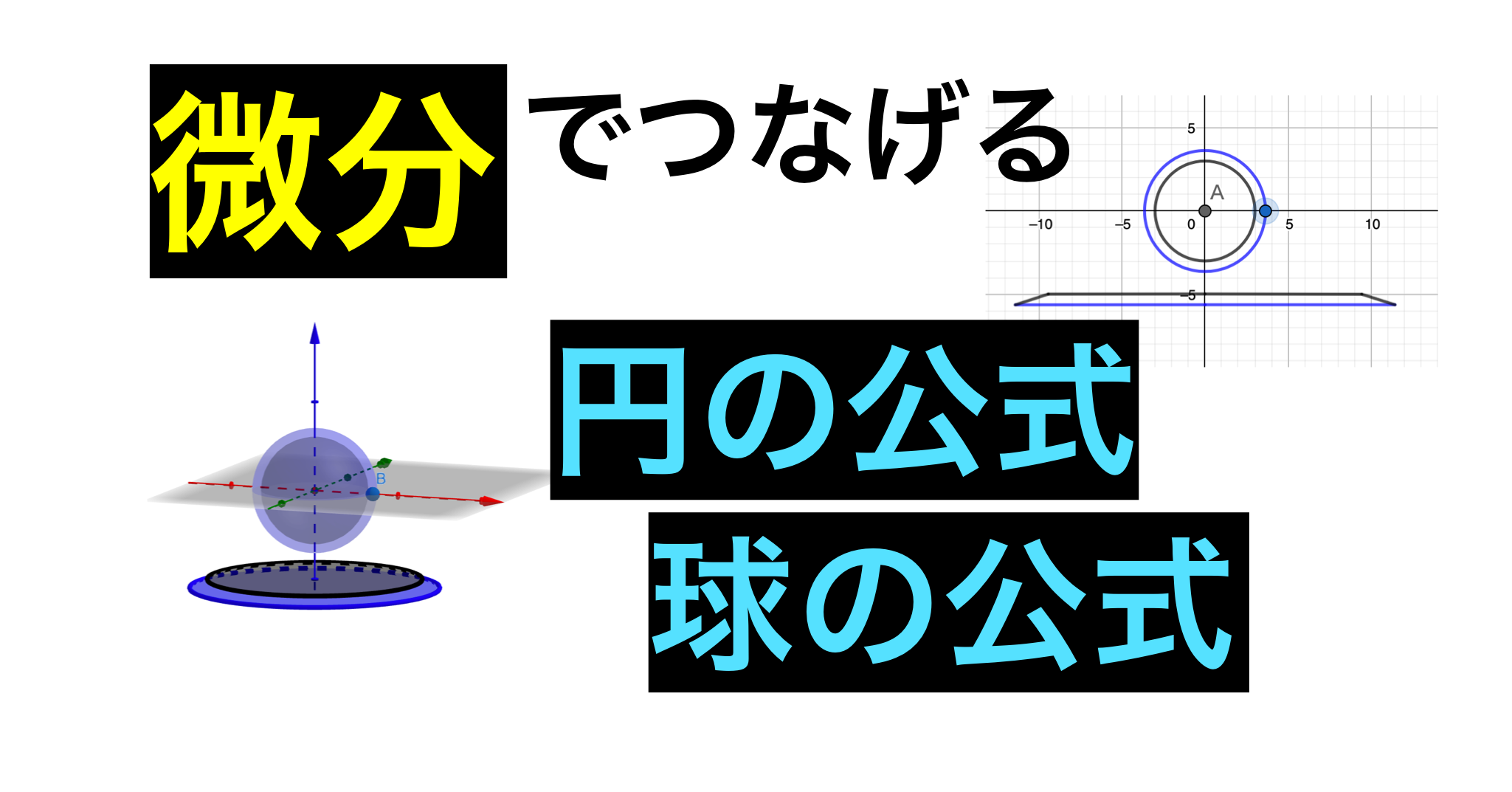


微分でつなげる円や球の公式 すうがくブログ 式変形ch



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の表面積と体積の公式 数学fun



初等幾何 球の表面積を求める 大人が学び直す数学



球の体積と表面積 公式と計算問題と証明 Irohabook



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ
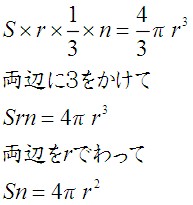


Mathematics 球の体積と表面積を求める公式 働きアリ



球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



球の体積 球の表面積の公式の導出 積分 優技録



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ


球の表面積の公式の覚え方 使い方を教えます スタモ 受験 入試 学習の総合サイト



球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく



球に関する公式 理数系無料オンライン学習 Kori



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



球の表面積の公式について みたにっき はてな



球の体積と表面積 Youtube


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



球の表面積と体積の公式 数学fun


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス
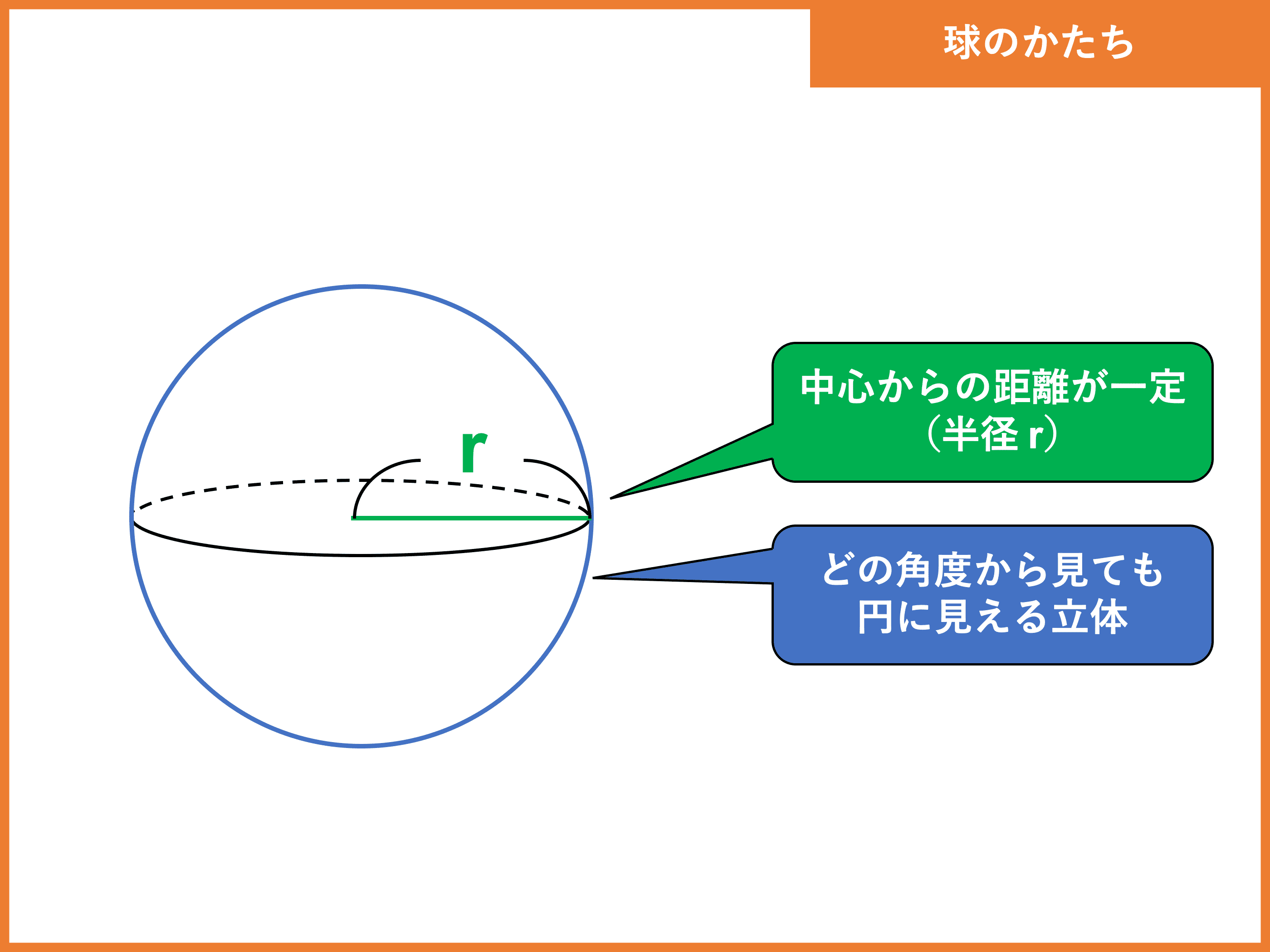


球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ


研究
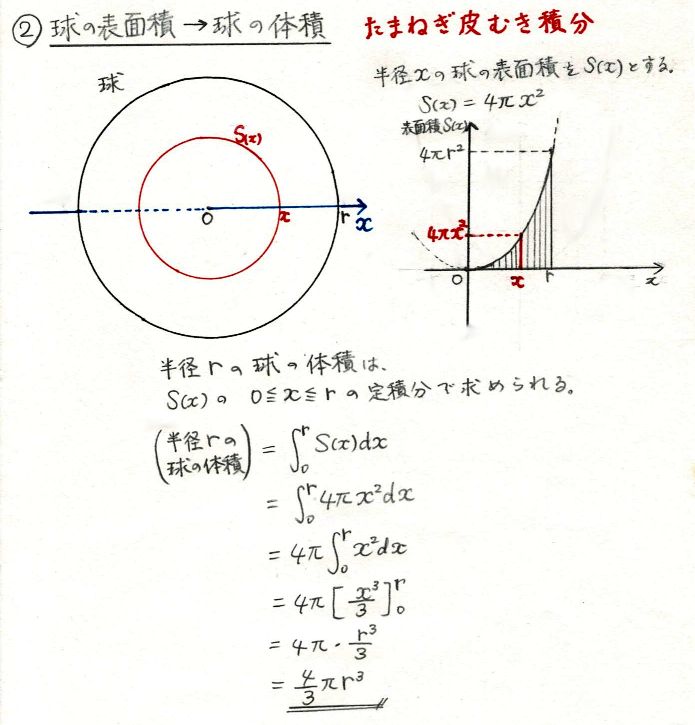


数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



角錐 円錐の体積と表面積の公式 数学fun


球の表面積の公式の導出 渋谷のaiメンターのブログ



球の表面積と体積の公式 数学fun



球の体積公式の微分が表面積になっている理由 Youtube


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



球の表面積と体積を求める公式 中学数学 By Okボーイ マナペディア



簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
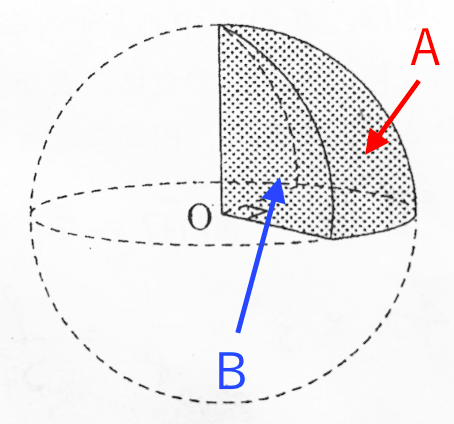


球の問題 苦手な数学を簡単に
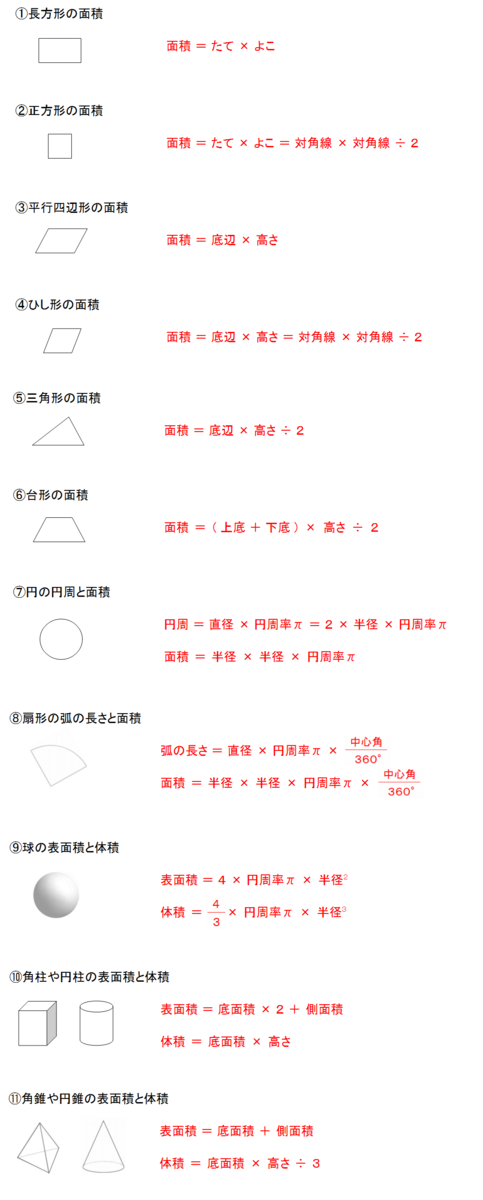


優雅 球体 表面積 求め 方 壁紙 配布


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



優雅 球体 表面積 求め 方 壁紙 配布



球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学
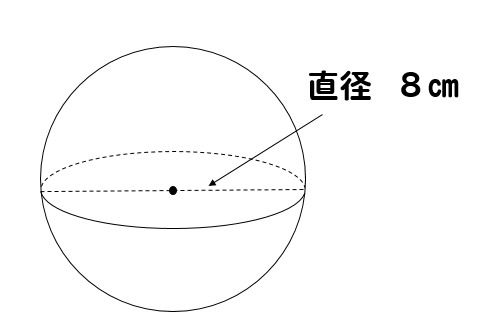


球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
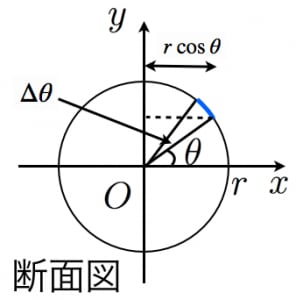


球の体積と表面積を積分で証明 高校数学の美しい物語



球の表面積の公式について みたにっき はてな



曲面 番外編 曲面の面積 身勝手な主張



球の表面積と体積の公式 数学fun


大学数学について球の表面積の公式を線積分を使って求めて下さい お願いし Yahoo 知恵袋



球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張


球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス



中1数学 球 映像授業のtry It トライイット



中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく


球の表面積の公式の求め方



球の表面積の公式と球の体積の公式 中学生の数学 要点 Yattoke 小 中学生の学習サイト
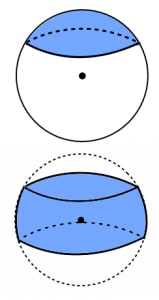


球欠 球台の体積と球冠 球帯の表面積 高校数学の美しい物語


Mathematics 球の体積と表面積を求める公式 働きアリ
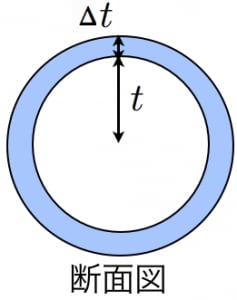


球の体積と表面積を積分で証明 高校数学の美しい物語


Math 円柱 内接する球 円錐の体積と表面積 働きアリ



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の表面積と体積の公式 数学fun



球の表面積と体積の求め方 苦手な数学を簡単に



球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
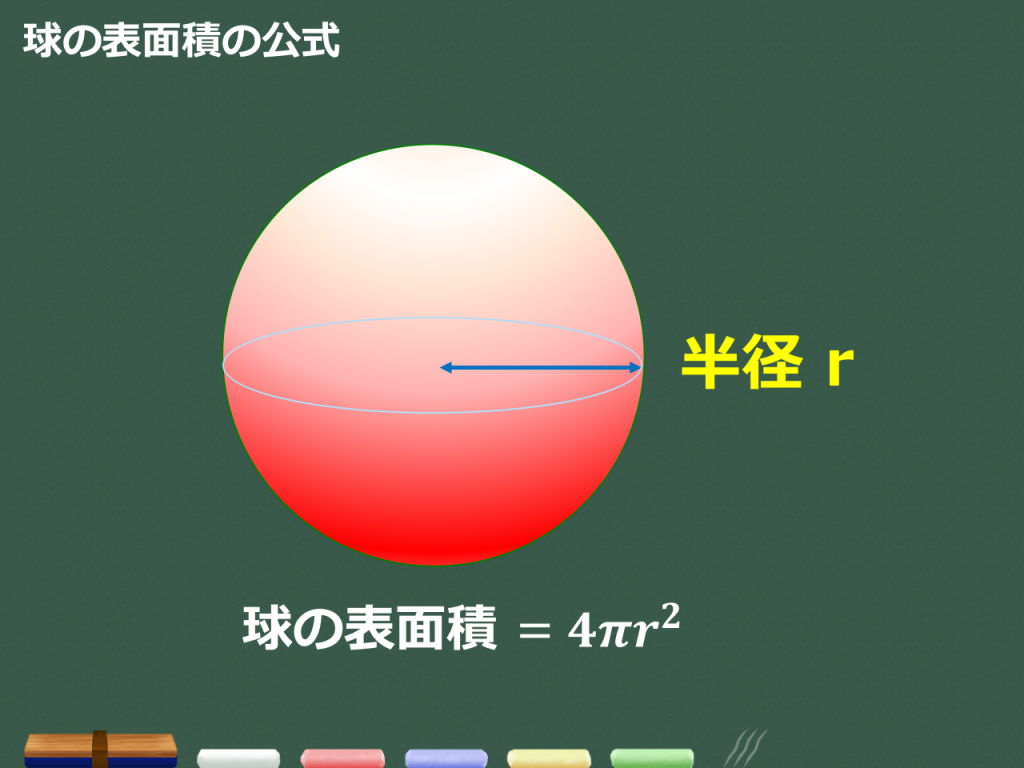


3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ



球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ


