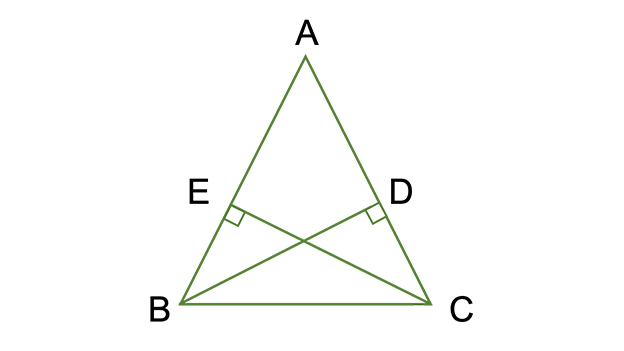
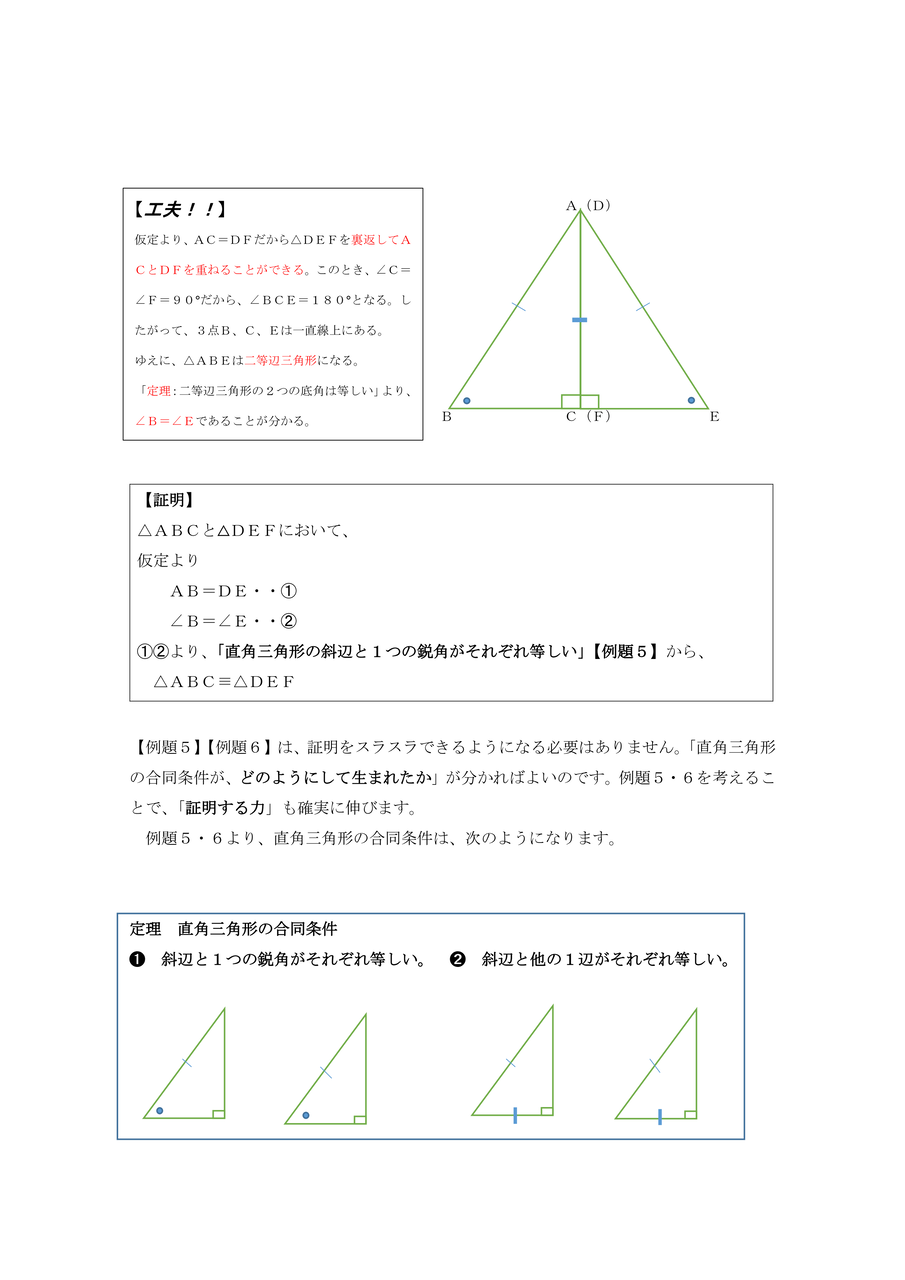
直角三角形の合同条件 平行四辺形の性質 平行四辺形になる条件 長方形とひし形 中点連結定理 平行線と距離 平行線と面積 2角が等しい三角形 正三角形 直角三角形の合同条件 平行四辺形の性質 平行四辺形になる条件 長方形とひし形 中点連結定理 平行線と距離 平行線と面積 直角三角形の合同条件を使う証明問題 ポイント まず、わかっていること、仮定からわかることを図示してみよう。 つまり、∠cae=∠daeを証明できればゴールなんだ! じゃ、どうするか・・・? 今まで学んできたように、三角形の合同条件を使うのが良さそうだ! でもね・・・もう一回三角形の合同条件を理解し,三角形が合同かどうかを対応する辺や角を示 もとに説明することができる。 B (良い) 三角形の合同条件を理解し,合同条件を示して三角形が合同かどうかを説 明することができる。 C Bに至らない。 (3)準備物 ワークシート,分度器,コンパス (4)学習の展開
1000以上直角三角形相似条件 ニスヌーピー壁紙
三角形 合同条件 直角三角形
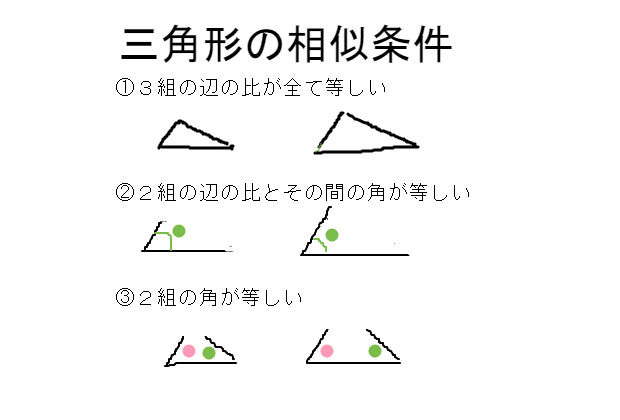
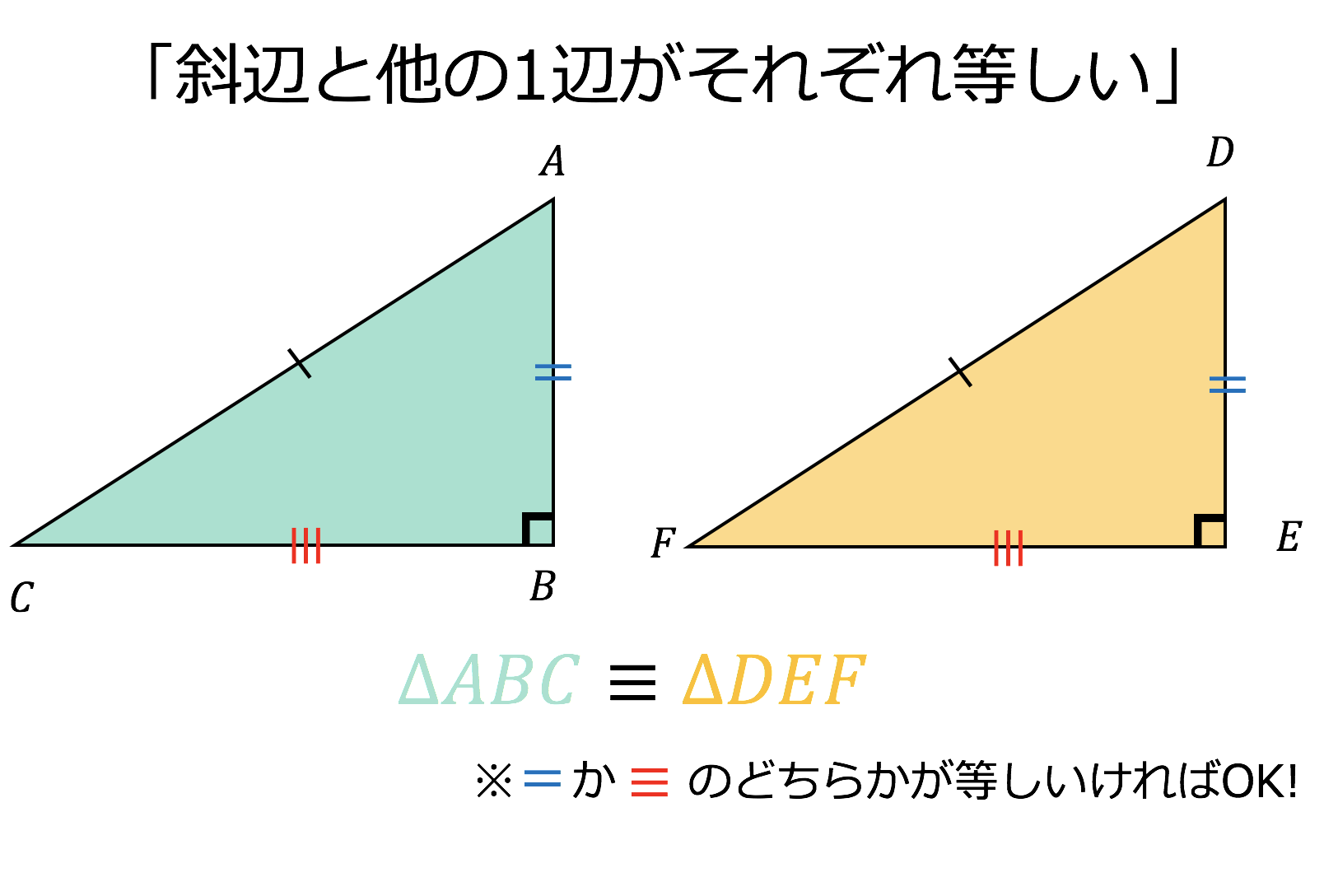
三角形 合同条件 直角三角形-2542 直角三角形の合同条件 問題 1 2つの三角形の合同条件は何でしょうか? 正解 : 直角三角形の斜辺と他の1辺がそれぞれ等しい。 (RHS) 問題 2 2つの三角形の合同条件は何でしょうか? 正解 :直角三角形の斜辺と1つの鋭角がそれぞれ等しい。 (RHA) 両方とも 数学の証明 のために必要なアイテムだから、テスト前には覚えなきゃいけないね。 念のためおさらいしておくと、 三角形の合同条件 3つの辺の長さがそれぞれ等しい 2組の辺の長さとその間の角が等しい 両端の角とその間の辺の長さがそれぞれ等しい 三角形の相似条件 3組の辺の比がすべて等しい 2組の辺の比とその間の角がそれぞれ等しい



三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト
直角三角形は、角の1つが直角であるために、合同条件は見た目が緩くなります。 合同条件は次の通りです。 直角三角形の合同条件 斜辺と他の1組の辺がそれぞれ相等しい 斜辺と直角でないの1組の角がそれぞれ相等しい それぞれ見ていきましょう。 斜辺と他の1辺 斜辺がそれぞれ相等しい 九年级数学直角三角形相似的判定ppt,直角三角形相似的判定 第三课时 执教者:邓玉春 已经学习的三角形全等的判定定理有: aas asa sas sss hl 已经学习的三角形相似的判定定理有: 两角对应相等,两三角形相似。 两边对应成比例且夹角相等,两三角形相似。三角形の合同条件 とは、 2つの三角形が合同であることを示すための条件 です。 以下の3つの合同条件のうち、どれかが成り立つ場合、その三角形は合同であるといえます。 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。
直角三角形の合同条件 直角三角形は,1つの角度が 9 0 ∘ 90^{\circ} 9 0 ∘ であるため,特有の合同条件を持ちます。鈍角三角形(どんかくさんかっけい、英 obtuse triangle )は、三角形の一種で、3つの角のうち、最大角または長辺に対する角が直角 (90° = π /2 rad) よりも大きい図形である。 なお、鈍角三角形では、長辺を c、短辺を a,b とすれば、各辺は c 2 > a 2 b 2 の関係となり、また外心や垂心が三角形の三角形の合同条件に関する史的考察(Ⅲ) ―高等小学算術書(国定)に関して一 中 西 正 治 (大阪府南河内郡美原町立西中学校) (1999年1月31日受付) 概 要本稿は,拙稿(1)(2)の続きにあたるもので,対象とした時代は国定算術書の時代である。本 稿は,その時代に使われた教科書の三角形 の合同条件 証明
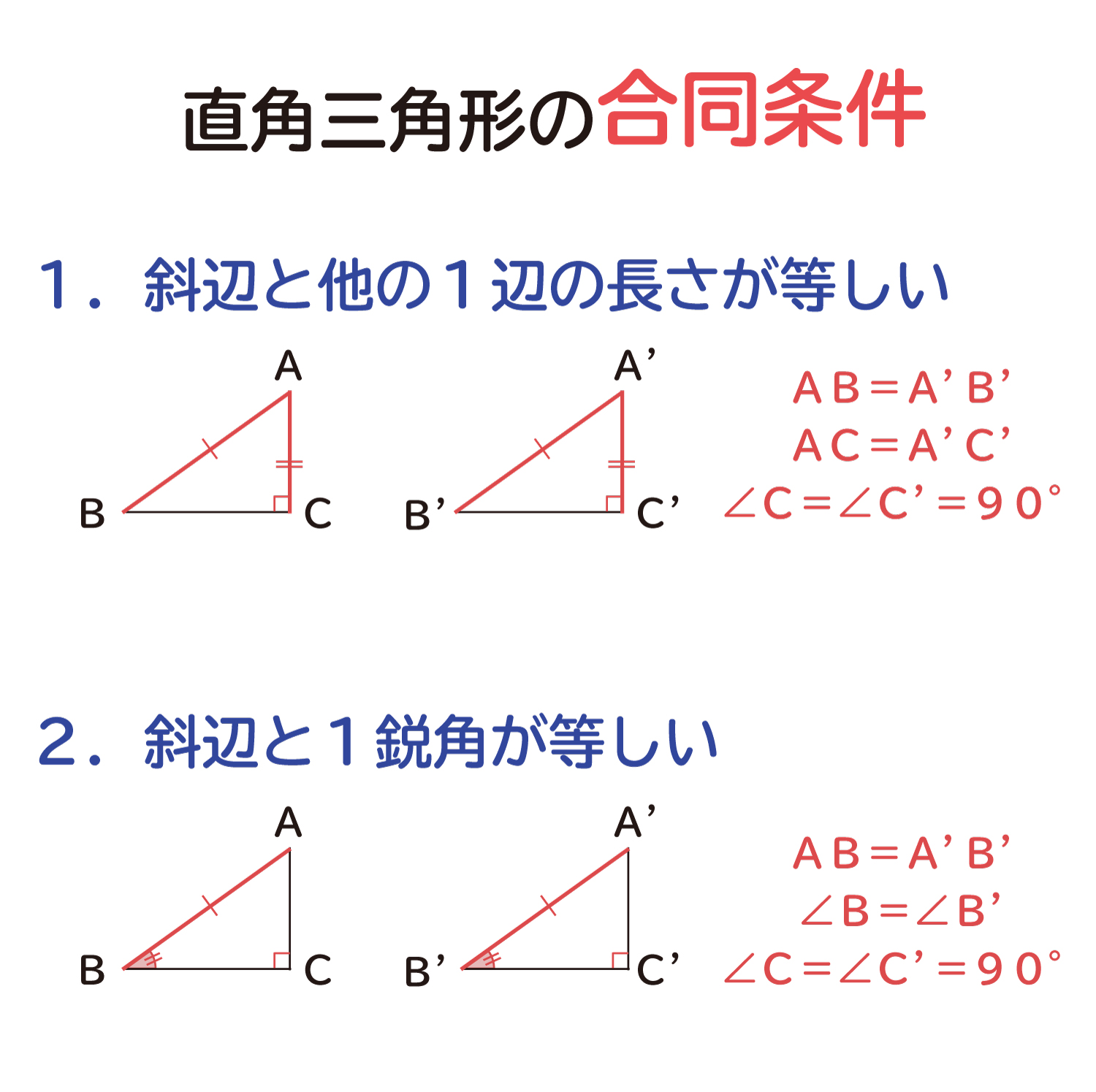
すると,$1$ 辺の長さとその両端の角がそれぞれ等しくなるので,三角形の合同条件の ($3$) を満たします.ゆえにふたつの直角三角形は合同です. 斜辺と他の一辺がそれぞれ等しい直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明) 直角三角形の合同条件とは 直角三角形は、以下のことが分かれば合同だと言えます。 今までの三角形の合同条件が このように、3つの情報を組み合わせて合同を言うことができましたが 直角三角形の場合には このように2つの情報だけでOKになります。 ちょっと便利ですね (^^) ただし、直角三角形の斜辺が等しいことが前提となっているので注意ですね。



最も人気のある 三角形合同証明 ニスヌーピー壁紙




人教版初三数学解直角三角形应用2下载 Ppt模板 爱问共享资料
三角形の合同条件 3組の辺がそれぞれ等しい 2組の辺とその間の角がそれぞれ等しい 1組の辺とその両端の角がそれぞれ等しい これから証明問題へ進んでいく上で 必要となってくるものなので ぜーーーーったいに覚えておきましょう! また、合同な 直角三角形の合同条件 2つの直角三角形において、次の2つの条件のうちどちらかが成り立つとき、その直角三角形は合同であるといえます。 斜辺と1つの鋭角がそれぞれ等しい 斜辺と他の1辺がそれぞれ等しい 直角三角形の証明問題直角三角形の合同条件では、この 「斜辺」 が主役。 「斜辺」 と 他の1辺 か、 「斜辺」 と 1つの鋭角 がそれぞれ等しければ合同になるんだ。



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
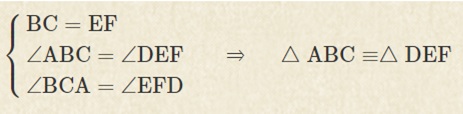



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
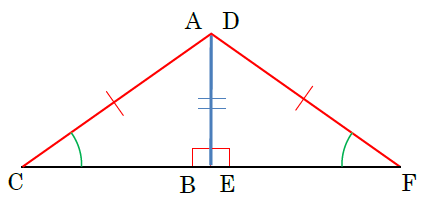
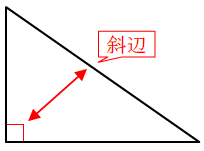
直角三角形の合同条件のポイントは! 直角三角形とは1つの角が直角である三角形のこと 直角の向かいにある辺のことを斜辺という 直角三角形の仮定と結論,逆,合同条件/三角形の合同の証明/二等辺三角形の定理/ 二等辺三角形の性質を使った証明 /二等辺三角形になることを証明/正三角形/ 直角三角形/ 平行四辺形の性質/平行四辺形になるための条件/長方形・ひし形・正方形/ 折り返し /平行線と面積/FdData 入試製品版三角形の合同条件 三角形の合同条件 合同とは 一方の図形を移動させて他方に重ね合わせることができる場合、この2つの図形は 合同 であるという。 三角形の合同を判断する場合、重ねあわせなくても下記の3つの合同条件のうちどれか一つに当てはまれば合同だといえる。




3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ




19 年九年级数学上册1 2直角三角形学案 无答案 北师大版下载 Word模板 爱问共享资料
中学2年生の課程で直角三角形の合同条件という定理がでてくる。 斜辺と1鋭角がそれぞれ等しい直角三角形は合同である 斜辺と他の1辺がそれぞれ等しい直角三角形は合同である この1つ目に疑問を持った方は多いと思う。これ,いらないんじゃないと。直角三角形の合同証明の書き方とは 直角三角形の合同条件を利用した、合同証明の問題に挑戦してみましょう。 二等辺三角形 三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。そ直角三角形とは?定義や定理、辺の長さの比、合同条件 🙌 直角三角形が2つくっついてる問題 つぎは、 直角三角形が2つくっついてる問題な。 問題1 この三角形は、正方形をひとつの対角線で分割してできるものです。 斜辺でない方の2辺の半円と直角




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく



直角三角形の合同条件
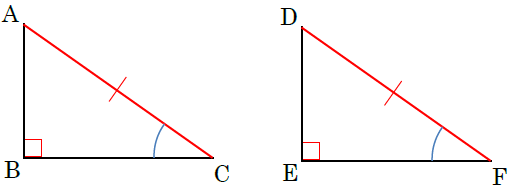
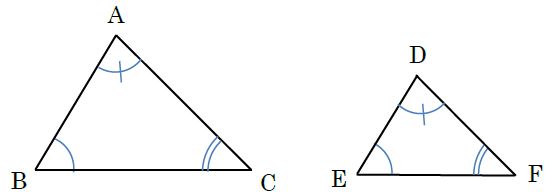
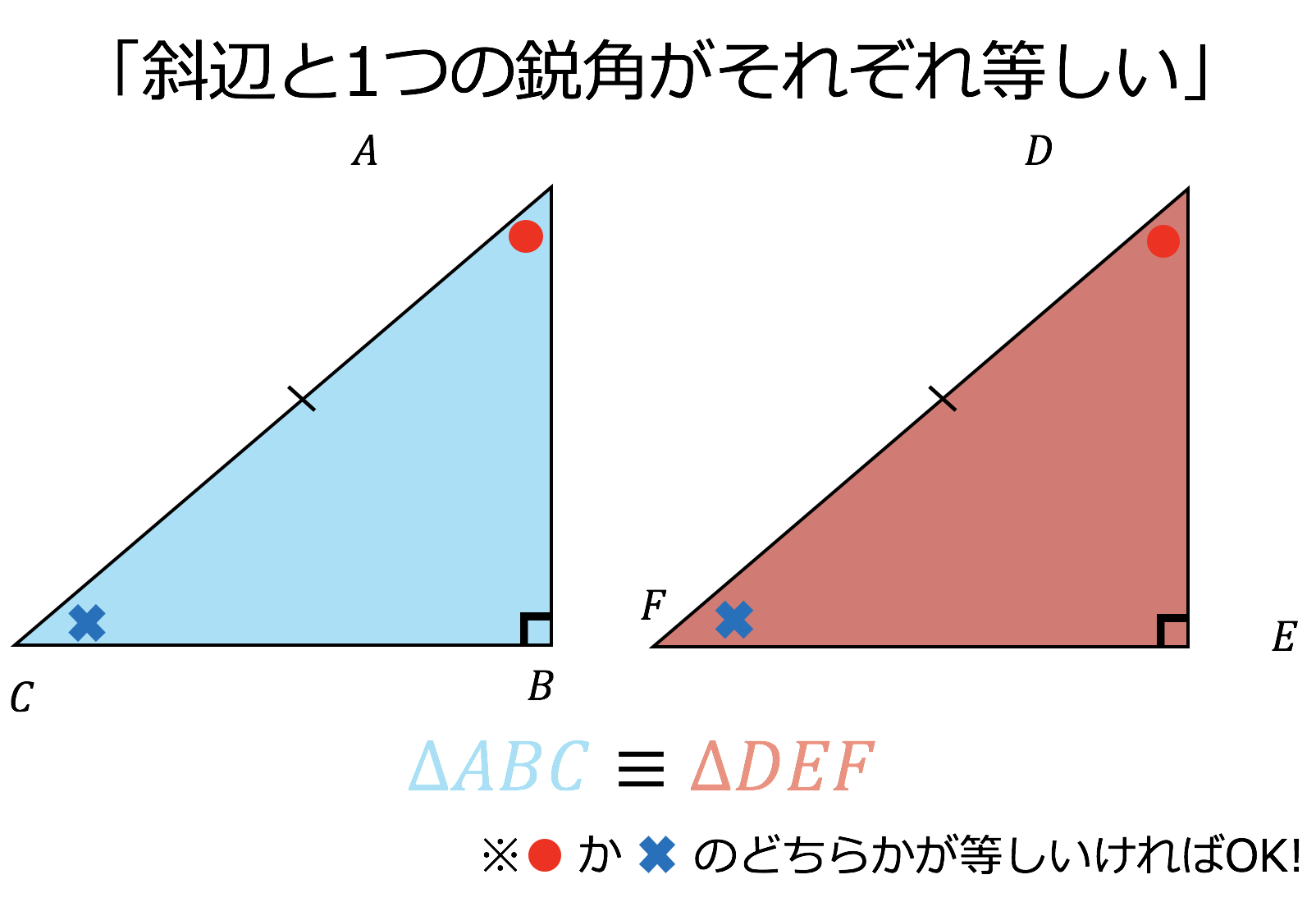
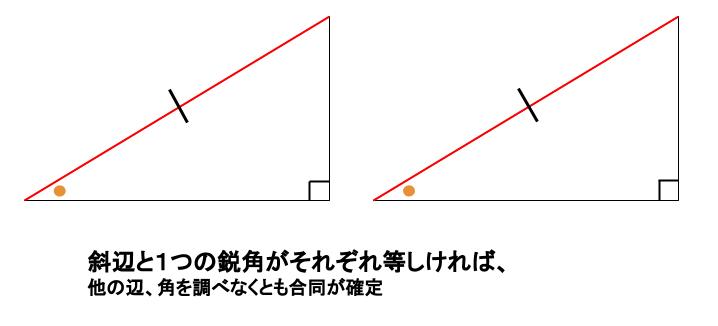
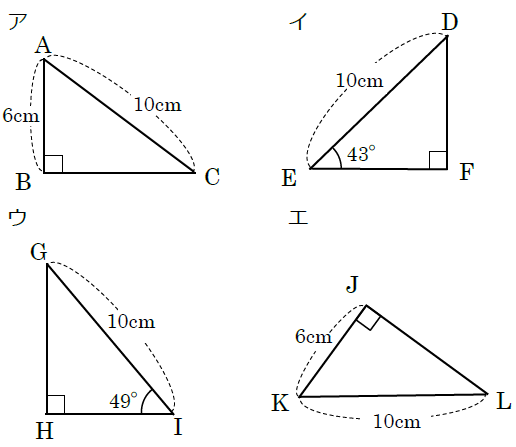
直角三角形の合同条件を使うときは,必ず斜辺の長さが等しいかどうか確認しましょう。 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年 中学1年~中学3年生 内容 計算の基礎養成演習 時間割 50分授業×週1回 授業回数 月間4回 授業料 中学1年生:8,300円 中学2年生:8,700円 直角三角形の合同条件には、以下の \(2\) つがあります。 条件①斜辺と 1 つの鋭角がそれぞれ等しい \(1\) つの角が \(90^\circ\) であることから、斜辺の長さおよび \(1\) つの鋭角が等しいことが示せれば、 残りの \(1\) 角も自ずと定まります 。直角三角形 合同条件 よって、合同条件「1組の辺とその両端の角がそれぞれ等しい」を満たします。 HI=LK=8cm、∠H=∠L=80°、∠I=∠K=30° なので 直角三角形の合同条件とは 直角三角形の合同条件は「普通の三角形の合同条件」に2つの条件が加わります。 全部で5つの条件があり、これらのうちどれか1つでもあてはまれば、「合同である」と言えます 直角三角形




中2数学 直角三角形の合同条件 Youtube



直角三角形の合同条件 まなびの学園
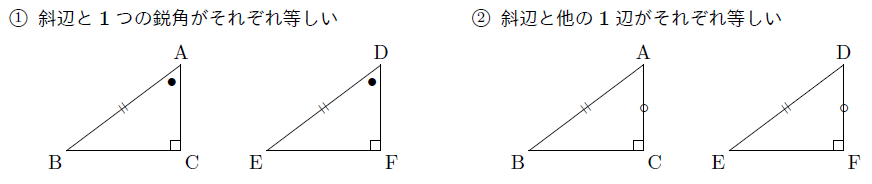
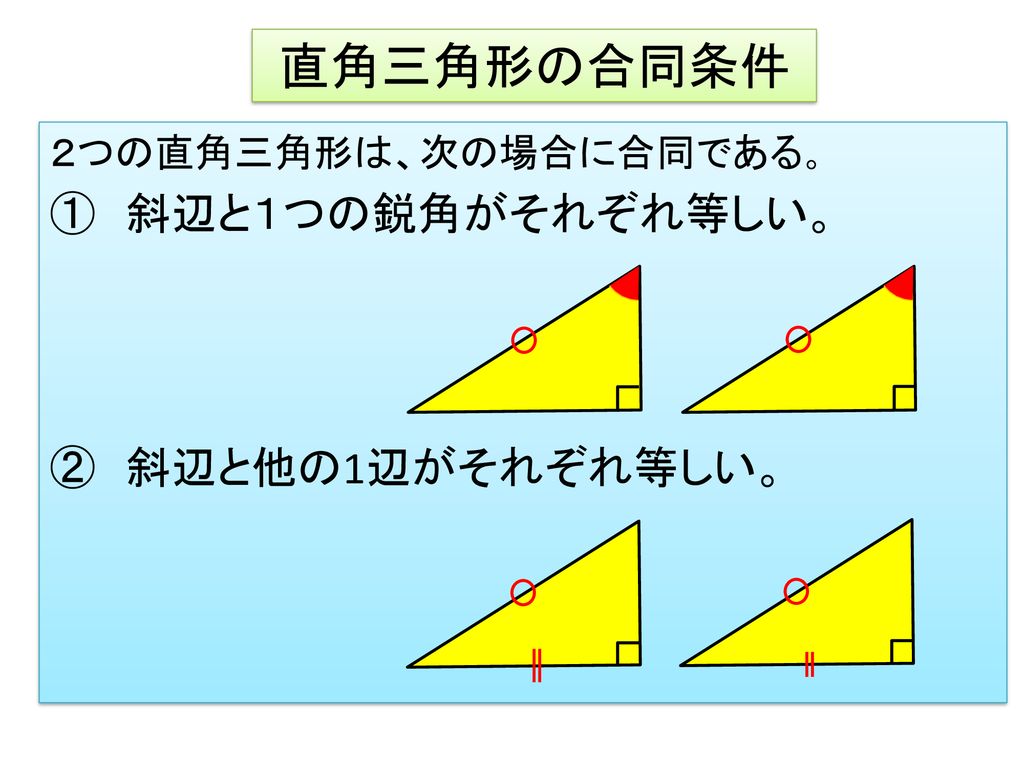
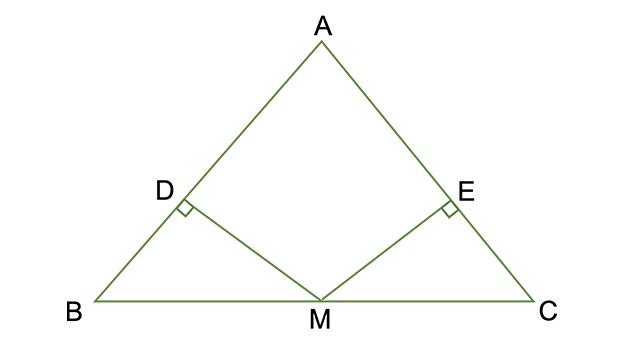
直角三角形の合同条件には次の \(2\) つがあります。 条件①斜辺と 1 つの鋭角がそれぞれ等しい \(1\) つの角が直角(\(90^\circ\))であることから、斜辺の長さおよび \(1\) つの鋭角が等しいことが示せれば、 残りの \(1\) 角も自ずと定まります 。 そのため、一般的な合同条件③「\(\bf{1}\) ここで三角形の合同条件を思い出して! 忘れた人はココ:三角形の合同条件 すると、 2組の辺とその間の角がそれぞれ等しい ので、 ade≡ acbとなる。 合同な図形では、対応する辺の長さが等しいので bc=edである。 ・・・(ここまでが答え)このとき、三角形の合同条件を参考にすることを確認する。 練り合う 数学的活動 〔観察、操作などの具体的な活動〕 ・斜辺と1つの鋭角がそれぞれ等しい場合と、斜辺と他の1辺がそれぞれ等しい 場合に分けて考える。 ・実際に、画用紙で作った直角
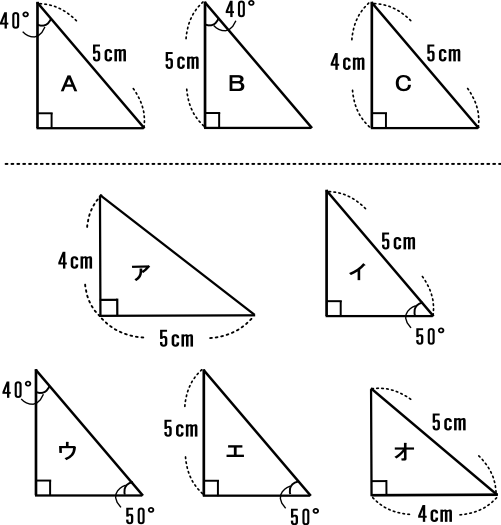



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく



直角三角形の合同条件は 市川中学 10年 算数解法の極意




三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学




中2数学 三角形と四角形 直角三角形の合同条件を利用した証明 二等辺三角形の頂点から垂線をひいたとき Youtube




人教版初三数学解直角三角形应用2下载 Ppt模板 爱问共享资料



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




直角三角形の合同条件 小学生 中学生の勉強




直角三角形の合同条件 証明のときに直角三角形が出てきたらこれ 中学や高校の数学の計算問題
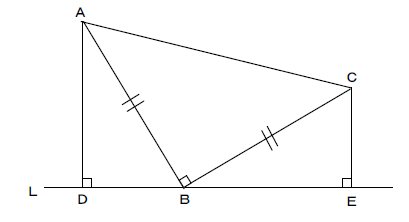



中2数学 直角三角形の合同証明のポイントと練習問題 Atstudier




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張
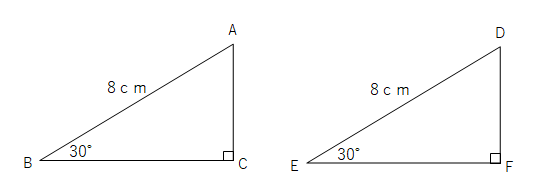



中2数学 直角三角形の合同証明のポイントと練習問題 Examee




直角三角形の合同条件とその証明 数学fun
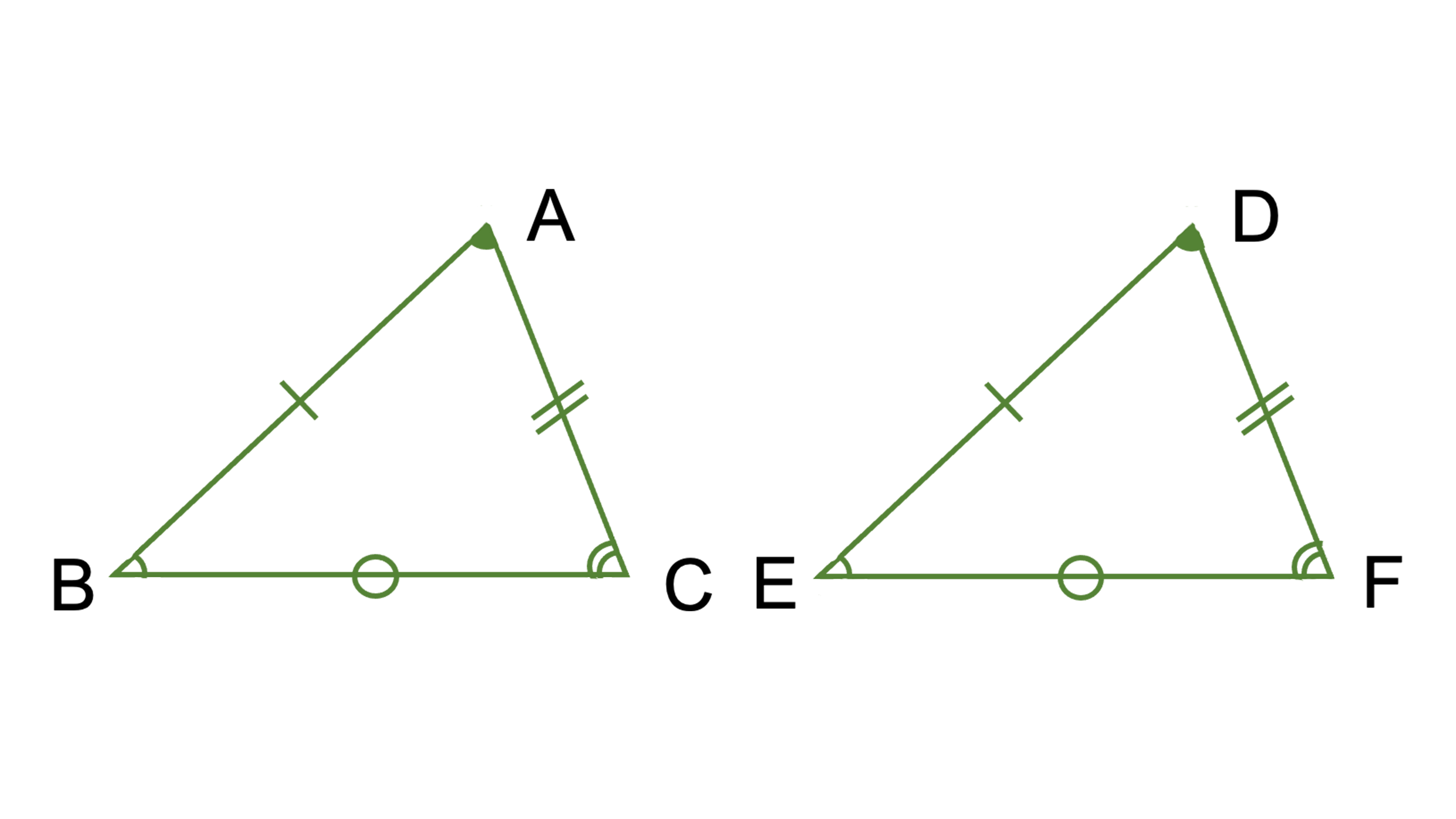



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




Junior High数学的中2 数学の世界直角三角形の合同条件筆記 Clear
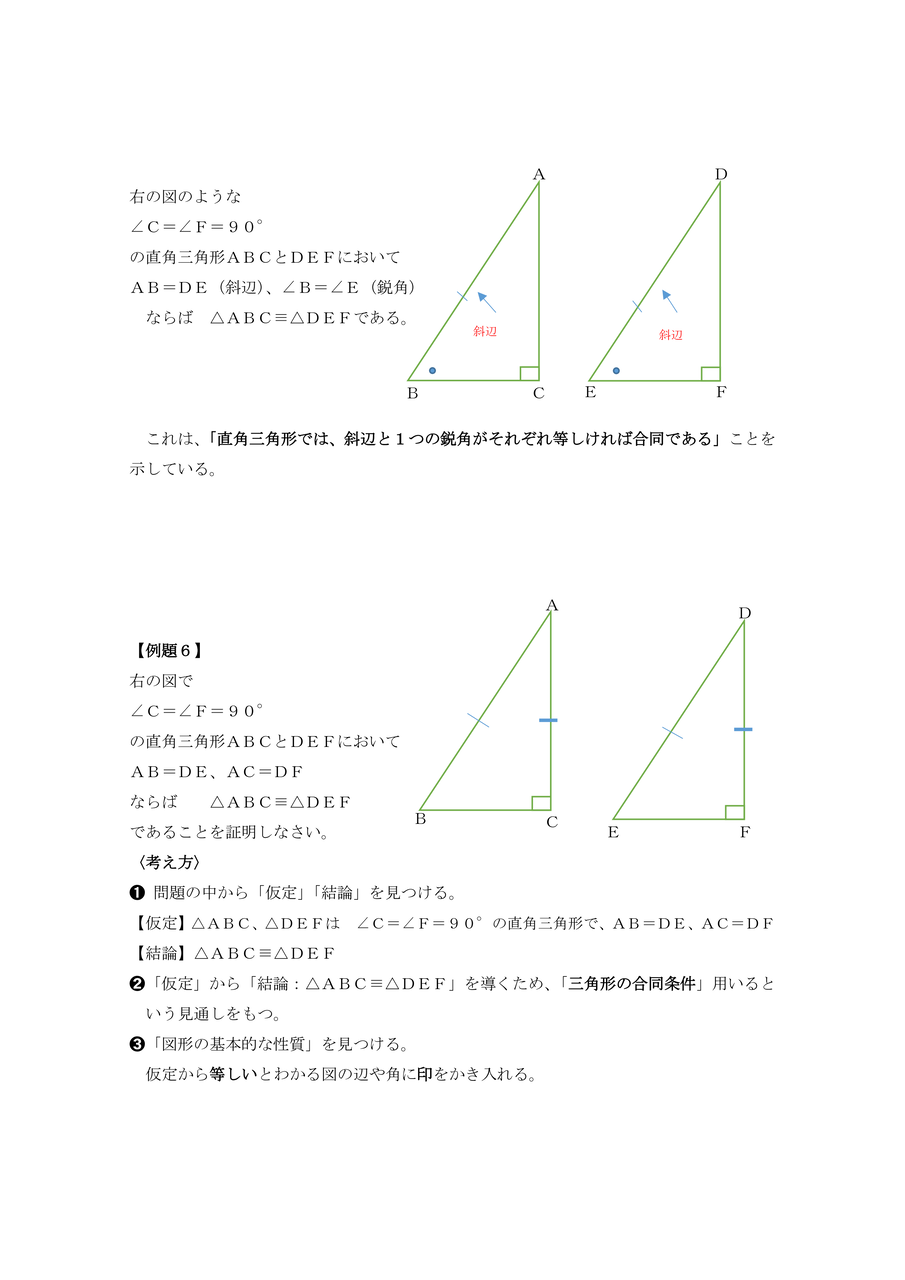



中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材




P130 Descubre Como Resolverlo En Qanda



1000以上直角三角形相似条件 ニスヌーピー壁紙
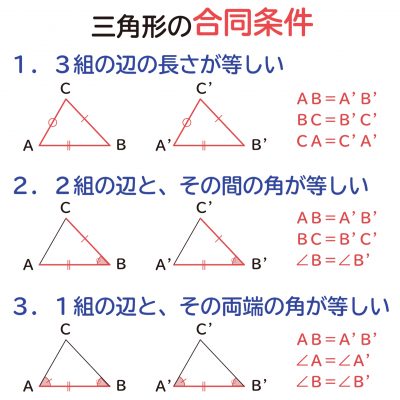



直角三角形の合同条件の説明 おかわりドリル



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



直角三角形の合同条件 On Vimeo



直角三角形の合同条件の説明 おかわりドリル




年春八年级数学下册第1章直角三角形1 2直角三角形的性质与判定 第3课时练习2 含解析 新版 湘教版下载 Word模板 爱问共享资料




3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ




2 の直角三角形の合同条件は何ですか 理由も付けて教えて頂けると助かります Clear



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ



本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download




北师大版九年级数学直角三角形 1 下载 Word模板 爱问共享资料




探索直角三角形全等的条件演示文稿下载 Ppt模板 爱问共享资料




三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
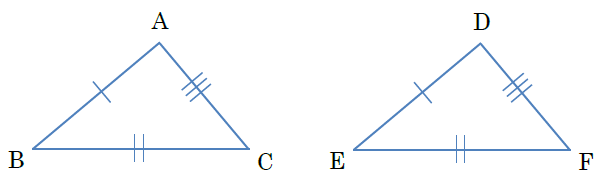



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




初中几何专练 三角形 做完这27道经典题 期末几何部分稳了 数学 直角 多边形 网易订阅




解直角三角形 专题复习 知识点 考点 测试 下载 Word模板 爱问共享资料
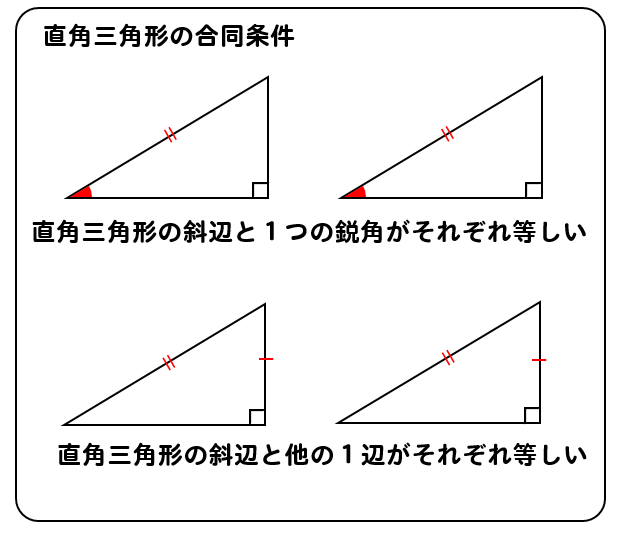



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ




中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材
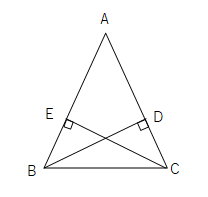



中2数学 直角三角形の合同の証明のポイントと練習問題 Pikuu



含30 锐角的直角三角形的性质下载 Word模板 爱问共享资料
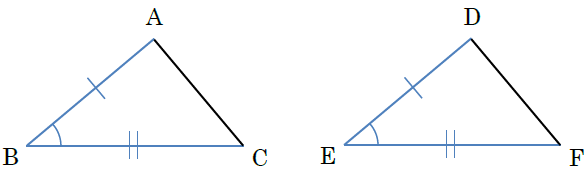



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




直角三角形の合同条件 Youtube
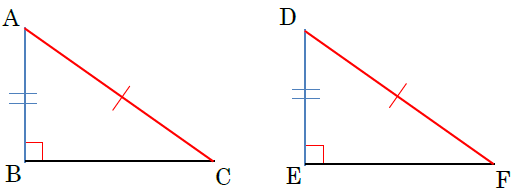



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



解直角三角形总结 解直角三角形总结精选八篇 范文118




中2数学 直角三角形の合同条件 例題編 映像授業のtry It トライイット




これは 直角三角形の合同条件を使っちゃいけないんですか Clear
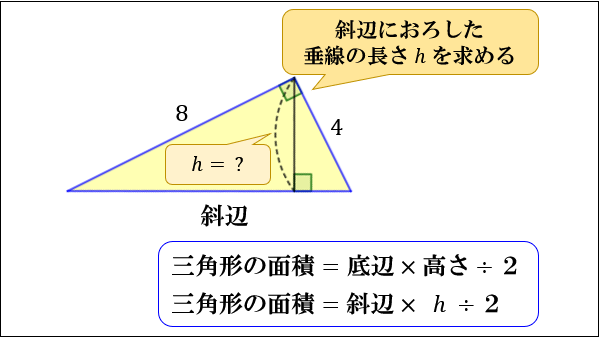



トップ100 正三角形面積小学生 最高のカラーリングのアイデア



直角三角形の合同条件とそれを利用した証明 チーム エン



証明直角三角形に三角形の合同条件 先程 直角三角形の証明を解いていて Yahoo 知恵袋




含30 角的直角三角形的性质 同步练习题下载 在线阅读 爱问共享资料




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張



股市中三角形形态整理 上升三角形 下降直角三角形详细介绍 上升三角形 零点财经
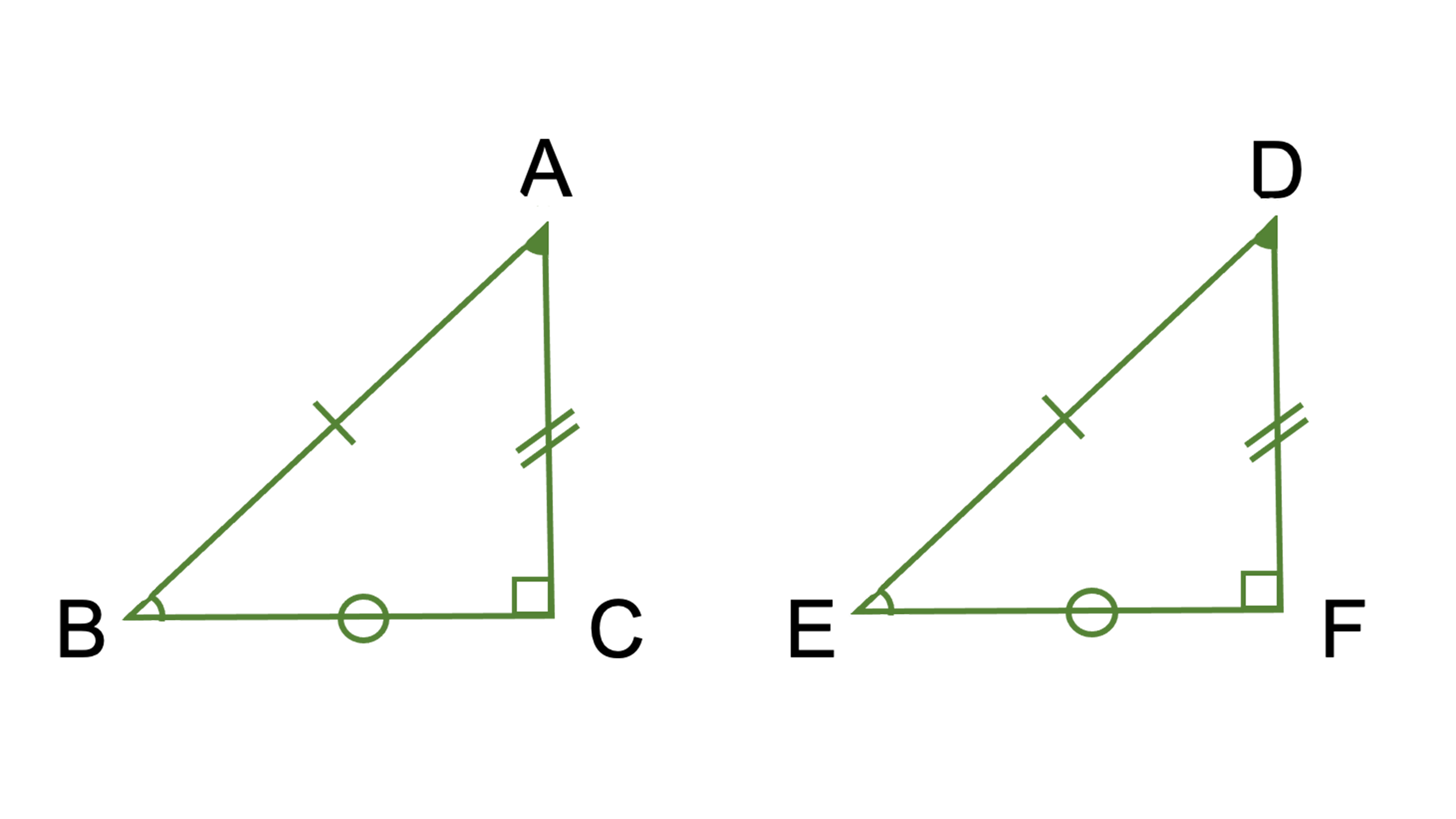



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




A Descubre Como Resolverlo En Qanda




中2数学 直角三角形の合同条件 例題編 映像授業のtry It トライイット



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中2 三角形の性質 直角三角形の合同条件 日本語版 Youtube



中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材




直角三角形存在性问题及真题典例分析 含解析 下载 Word模板 爱问共享资料




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく




直角三角形の合同の証明の問題です わからないので教えてください お願いします Clear
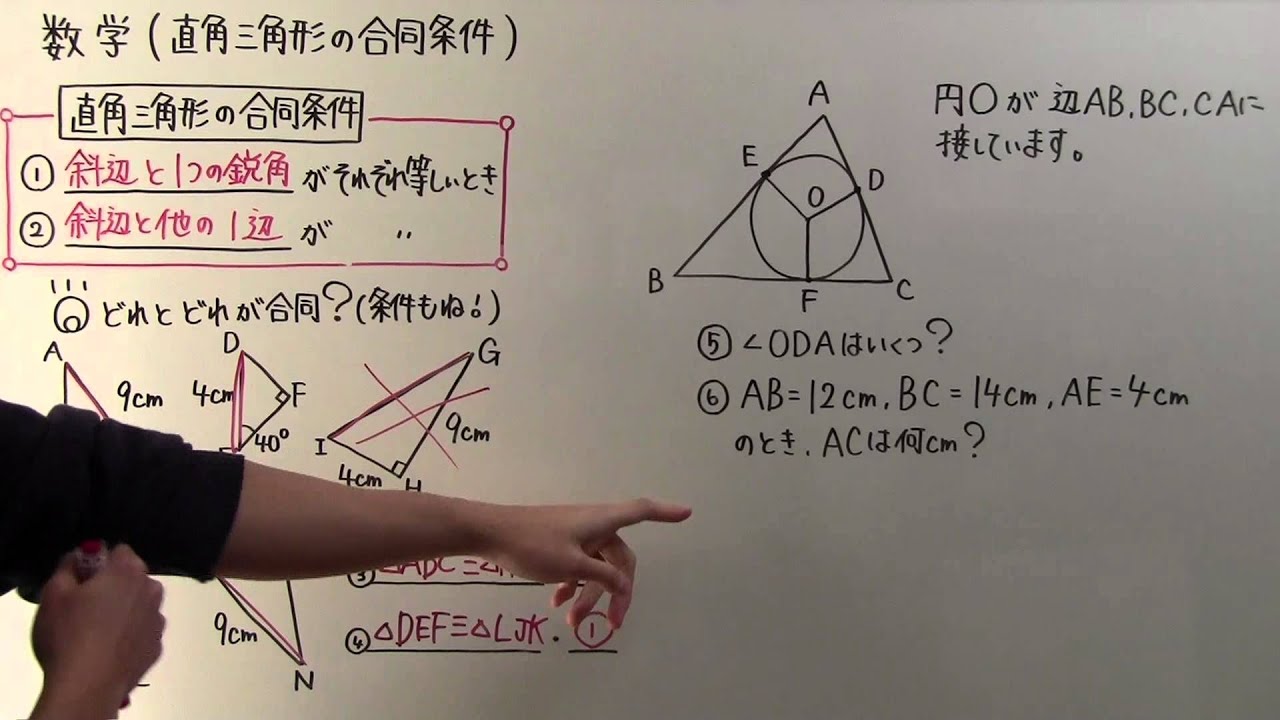



数学 中2 71 直角三角形の合同条件 Youtube
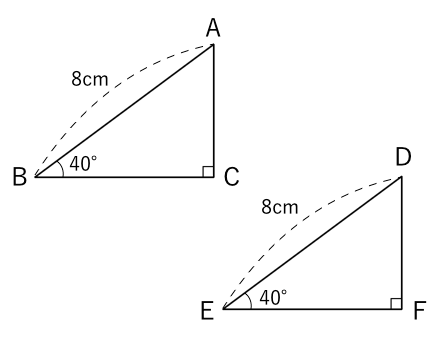



直角三角形の合同 条件 について 苦手な数学を簡単に




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
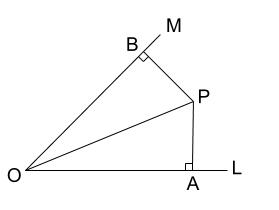



中学数学 直角三角形の合同の証明 中学数学の無料オンライン学習サイトchu Su




全等三角形hl判定的基本练习下载 Word模板 爱问共享资料




中考数学 二次函数与等腰直角三角形存在性问题 题型变幻莫测 解析式 勾股定理 抛物线 网易订阅
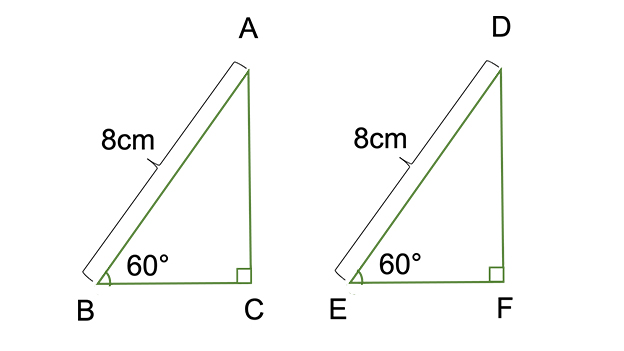



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材




中考数学 二次函数与等腰直角三角形存在性问题 题型变幻莫测 解析式 勾股定理 抛物线 网易订阅




本時のねらい 直角三角形の合同条件を導き それを理解し 証明ができるようにする Ppt Download




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく




已经三角形两边求第三边 知道三角形的两边求第三边 怎么求 三人行教育网 Www 3rxing Org




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋




授業料無料 中2数学 直角三角形の合同条件2 連問1 Youtube



3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




直角三角形の合同条件 小学生 中学生の勉強




初三数学解直角三角形下载 Word模板 爱问共享资料
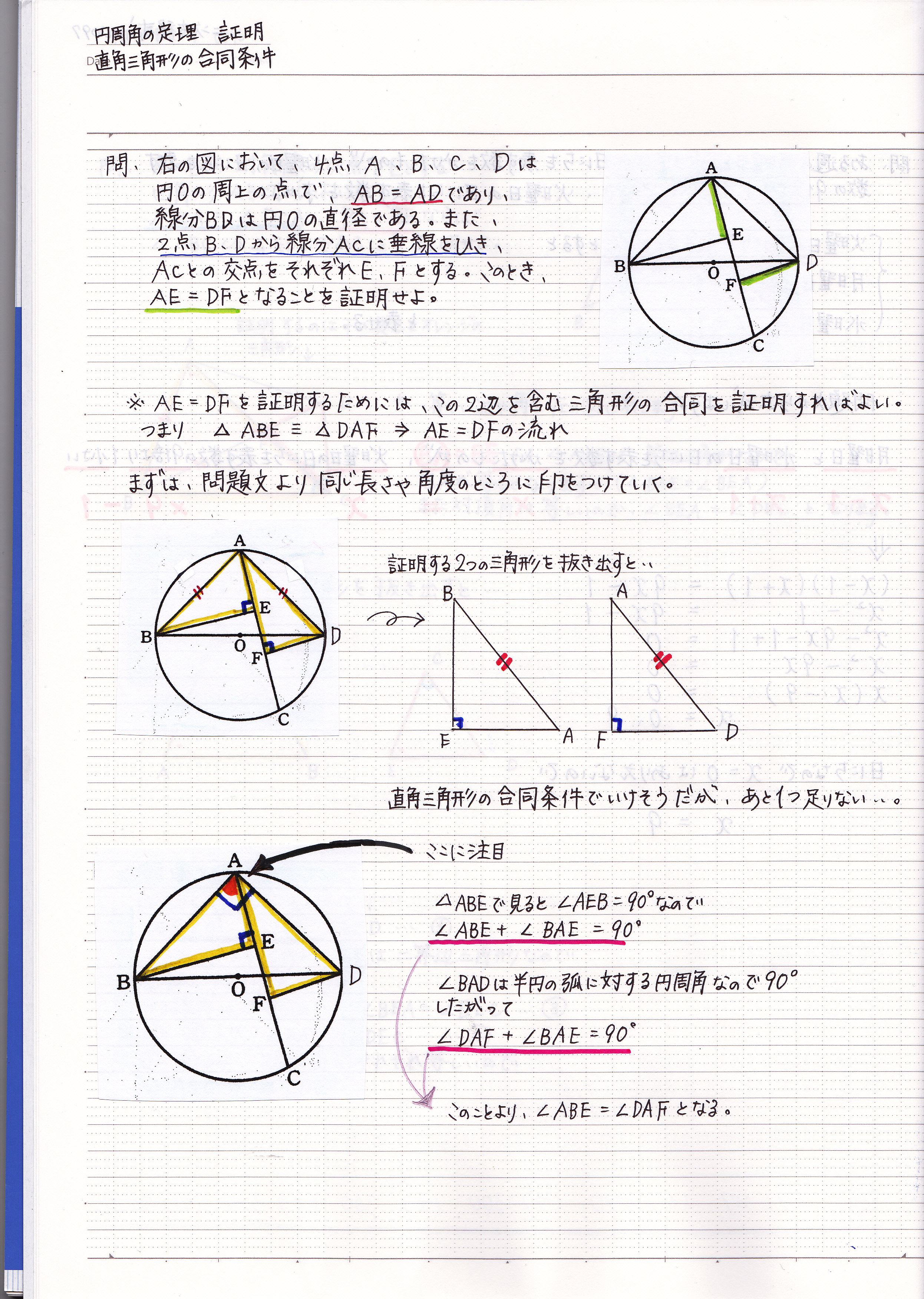



直角三角形の合同条件を使った証明問題の解き方 現役塾講師のわかりやすい中学数学の解き方
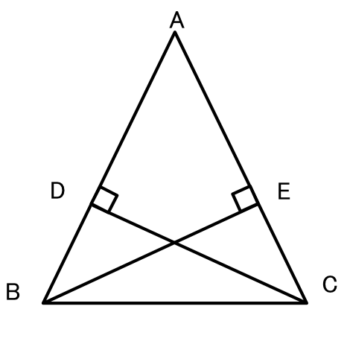



フロー 2 5 4 4 直角三角形の合同条件を利用した証明
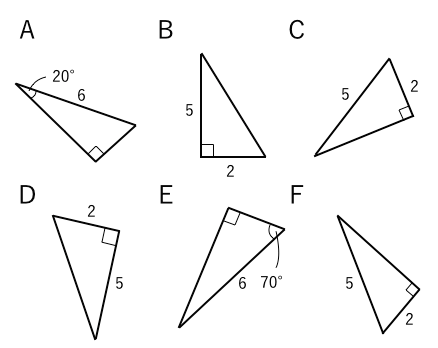



直角三角形の合同 証明問題 苦手な数学を簡単に




直角三角形の合同条件の証明 Youtube
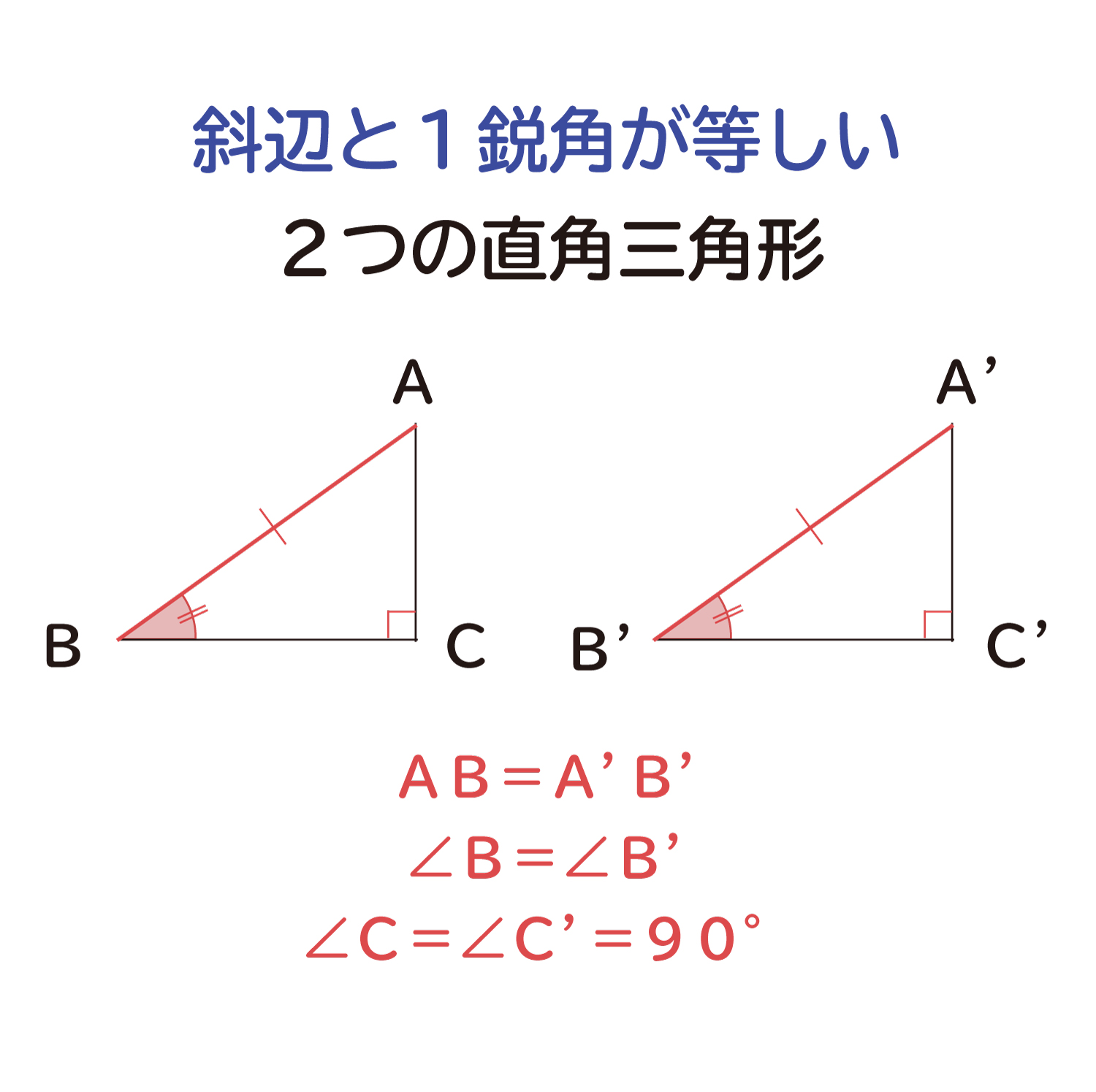



直角三角形の合同条件の説明 おかわりドリル



上数学合同条件 ニスヌーピー壁紙




直角三角形の合同条件 算数 数学が好きになりmath



直角三角形の合同条件の説明 おかわりドリル


