Explanation To graph a linear equation we need to find two points on the line and then draw a straight line through them Point 1 Let x = 0 0The graph of a linear equation is a straight line To locate that straight line you just need two points and solve the equation to find the corresponding value for the other variable You can chose any value, for any variable, but a smart choice makes the Draw the graph of each of the following linear equations in two variables i) x y = 4 ii) x y = 2 iii) y = 3x iv) 3 = 2x y The graph of the line represented by the given equation is

Draw A Graph X Y 4 And X Y 2 Brainly In
Linear equations x y 2 graph
Linear equations x y 2 graph-When x = 3, y = 3 2 = 5 Plotting the points ( 1 , 3 ) , ( 2 , 4 ) and ( 3 , 5 ) on the graph paper and drawing the line joining them, we obtain the graph of the line represented by the given equationGraph each linear equation xy=2 Get the answers you need, now!
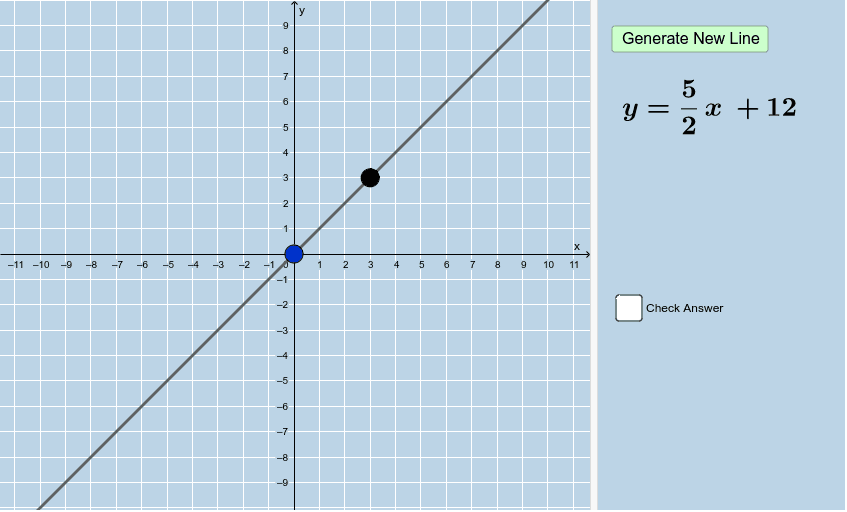



Kopi Av Kopi Av Quiz Graphing Linear Equations V1 Geogebra
Graph the equation \(y=\frac{2}{3}x1\) This equation is already in SlopeIntercept Form The slope is identified as m equals twothirds m=23 and the yintercept is at the ordered pair, (0, negative 1) (0,1) That is where the graphing begins Plot the first point at the yintercept, then move from that point according to the slopeAnswer to Graph the equation x = y 2 By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also askFree linear equation calculator solve linear equations stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy
Graph each linear equation y=x2 Draw the graph of each of the following linear equations in two variable xy=2Graphing linear equations y5=2(x2) Solve the following simultaneous linear equations in two variables by the method of elimination (xSince, as we just wrote, every linear equation is a relationship of x and y values, we can create a table of values for any line These are just the $$ x $$ and $$ y $$ values that are true for the given line In other words, a table of values is simply some of the points that are on the line
STEP 2 Using the equation y = 2x 1, calculate the value of y by using the x value in the table In this instance, x=0 How to draw a graph of a linear equationLet's do a couple of problems graphing linear equations and there are a bunch of ways to graph linear equations and what we'll do in this video is kind of the most basic way where we'll just plot a bunch of values and then connect the dots and I think you'll see what I'm saying so here I have an equation a linear equation I'll rewrite it just in case that was too small y is equal to 2x plus 7SOLUTION Graph linear equation xy=2 Thanks You can put this solution on YOUR website!




Math 11 Unit 7 Systems Of Linear Equations




X Y 2 Graph The Linear Equation Chavachel
In this video I show you how to graph the line y = 2x 2If you want your question answered in that next video, email it to mathhelpchannel@gmailcom in te38 EXEMPLAR PROBLEMS The graph of the linear equation 3x 4y = 12 cuts the yaxis at the point where x = 0 On putting x = 0 in the given equation, we have 4y = 12, which gives y = 3 Thus, the required point is (0, 3) Sample Question 2 At what point does the graph of the linear equation x y = 5 meet a line which is parallel to the yaxis, at a distance 2 units from the originFree graphing calculator instantly graphs your math problems




Systems Of Linear Equations Free Math Help




S Graph 3xy 2 T6 X Y 2 6 Write The Equation In Chegg Com
3 Graphical Solution of a System of Linear Equations A `2 ×2` system of equations is a set of 2 equations in 2 unknowns which must be solved simultaneously (together) so that the solutions are true in both equations We can solve such a system of equations graphicallyThat is, we draw the graph of the 2 lines and see where the lines intersect This time it is x's value that is 0Any where you would cross the yaxis, x's value is always 0We will use this tidbit to help us find the yintercept when given an equation Below is an illustration of a graph of a linear function which highlights the x and y interceptsAlgebra Graphs of Linear Equations and Functions Graphs of Linear Equations 1 Answer



Graphing Systems Of Linear Equations




Draw The Graph For Each Of The Equation X Y 6 And X Y 2 On The Same Graph Paper And Find The Co Ordinate Maths Linear Equations In Two Variables Meritnation Com
Using Intercepts to Graph Lines You can use intercepts to graph linear equations Once you have found the two intercepts, draw a line through them Let's do it with the equation 3y2x= 6 3 y 2 x = 6 You figured out that the intercepts of the line this equation represents are (0,2) (Graphing a Linear Function Using yintercept and Slope Another way to graph linear functions is by using specific characteristics of the function rather than plotting points The first characteristic is its yintercept which is the point at which the input value is zero To find the yintercept, we can set latexx=0/latex in the equationGraph functions and relations In order to graph a linear equation we work in 3 steps First we solve the equation for y Second we make a table for our x and yvalues From the x values we determine our yvalues Last we graph our matching x and yvalues and draw a line We are going to graph the equation 4x2y=2



X Y 2 Graph The Linear Equation Mathskey Com
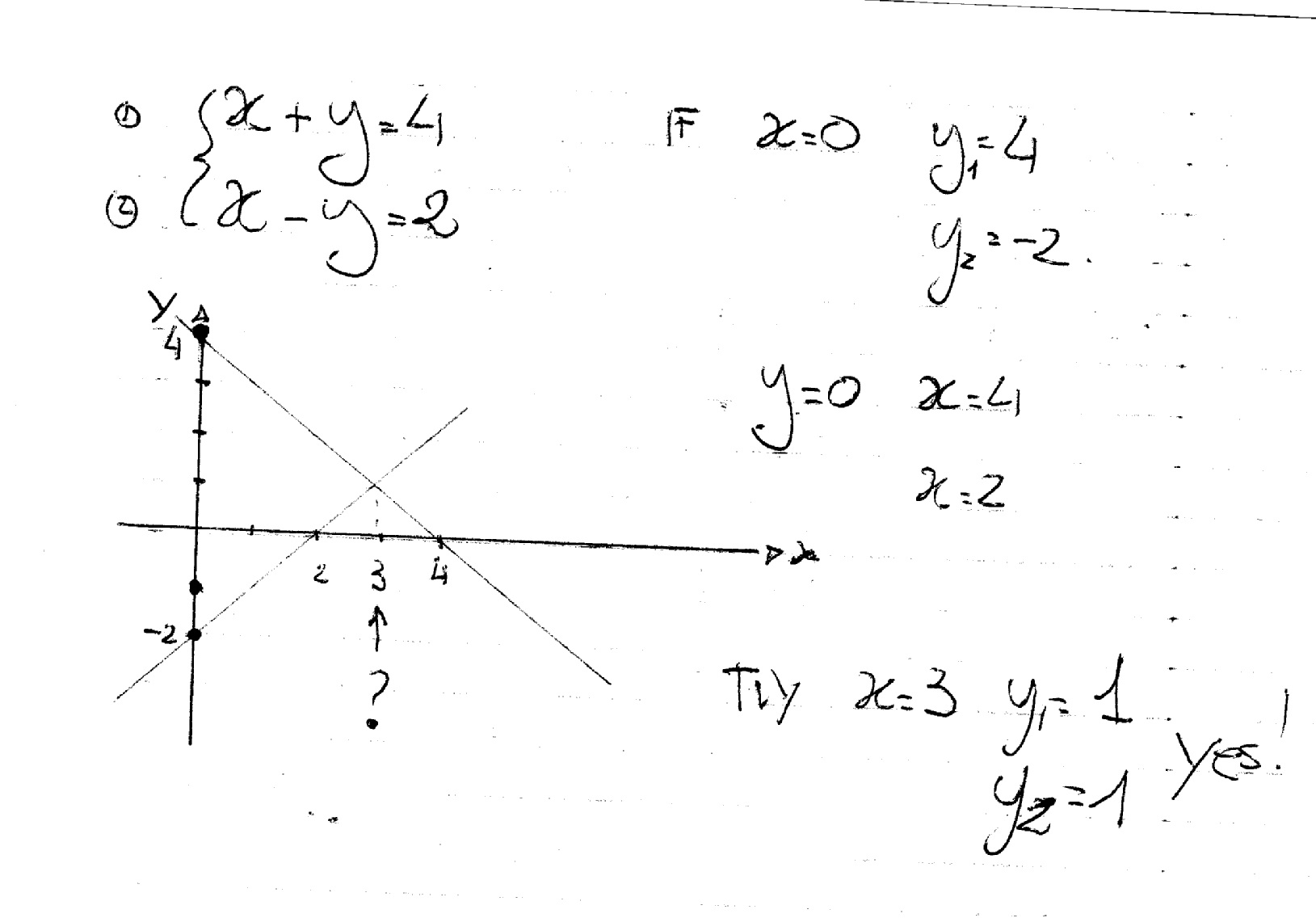



How Do You Solve X Y 4 And X Y 2 By Graphing Socratic
Draw the graph of the following linear equations in two variables xy = 2 Get the answer to this question and access a vast question bank that is tailored for studentsMethod 3 Using the x and yintercepts When graphing linear equations that are given in the form y = m x b, it is easiest to just apply method 2 But sometimes, linear equations are given in standard form A x B y = C, where A, B, and C are positive or negative whole numbers In this case, using the x and yintercept may be the quickestIf b ≠ 0, the equation = is a linear equation in the single variable y for every value of xIt has therefore a unique solution for y, which is given by = This defines a functionThe graph of this function is a line with slope and yintercept The functions whose graph is a line are generally called linear functions in the context of calculus




Ex 4 3 1 I Draw The Graph Of Linear Equation X Y 4 Teachoo




Kopi Av Kopi Av Quiz Graphing Linear Equations V1 Geogebra
For example, x2y = 6 is a linear equation and some of its solution are (0,3),(6,0),(2,2) because, they satisfy x2y = 6 Graphing of Linear Equation in Two Variables Since the solution of linear equation in two variable is a pair of numbers (x,y), we can represent the solutions in a coordinate plane Consider the equation, 2xy = 6 —(1) Graph the linear equation by using slopeintercept method The equation x y = 2 Write the above equation in slopeintercept form y = mx b, where m is slope and b is yintercept Now the equation is y = x 2 Slope m = 1 and yintercept b = 2 yintercept is 2, so the line crosses the yaxis at (0, 2) Using slope find the next pointDraw the graph of each of the following equations 2 x y = 5 In each case verify that i) Every point on the line satisfies the equation ii) Every solution of the equation is a point on the line iii) Any point which does not lie on the line is not a solution of the equation




Graphing Linear Equations What Is A Linear Equation A Linear Equation Is An Equation Whose Graph Is A Line Linear Not Linear Ppt Download




Draw The Graph Of Linear Equations X Y 6 And X Y 2 On The Same Graph Paper And Find The Coordinates Of Brainly In
That is, every solution of y = x 2 lies on the line, and every point on the line is a solution of y = x 2 The graphs of firstdegree equations in two variables are always straight lines;Therefore, such equations are also referred to as linear equationsSo our equation is two x two x plus Why back to me, right This two x plus y, um equals six So let's find her Why attacked our y intercept by making X zero are accidents that by making y zero and then a random other point which let's go ahead and make it, um, accidentally is too So, um, let's think x zero first So to time zero plus Weichel six now, two times zero is zero in
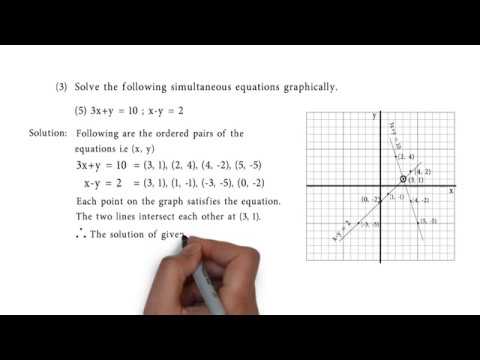



3x Y 10 And X Y 2 Problem Set 1 Q3 5 Of Linear Equations In Two Variables Youtube



1
Solve each system by graphing { x = 4 3 x − 2 y = 24 { x = 4 3 x − 2 y = 24 In all the systems of linear equations so far, the lines intersected and the solution was one point In the next two examples, we'll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutionsFor x = 4, y = 4, therefore (4, 4) satisfies the linear equation y = x By plotting the points (1,1) and (4, 4) on the graph paper and joining them by a line, we obtain the graph of y = x The given equation is y = – x To draw the graph of this equation, we need at least two points lying on the given line For x = 3, y = – 3, therefore, (3Any equation that can be represented in the form of ax by c =o, where a,b, and c are real numbers and a, b are not equivalent to 0 is known as a linear equation in two variables namely x and y The solutions for such types of equations are a pair of values, one for x and one for y which makes the two sides of the equation equal



Draw The



Solution Solve By Graphing X Y 2 X Y 8 Would It Be 2x 10
Ex 43, 1Draw the graph of each of the following linear equations in two variablesx y = 4x y = 4To draw the graph, we need at least two solutions of the equation Plotting pointsGraphing Linear Equations With Microsoft Excel Mr Clausen Algebra II STEP 1 Define Your Coordinates WHAT TO DO Set up your Excel spreadsheet to make a chart of points for and a graph of a linear equation The equation we'll be modeling in this lesson is y = 2x – 5 1Open Microsoft Excel In cell A1, type this text Graph of y = 2x 5Register for FREE at http//deltastepcom or download our mobile app https//bitly/3akrBoz to get all learning resources as per ICSE, CBSE, IB, Cambridge &



Draw The Graph Of The Linear Equation Whose Solutions Are Represented By The Points Having The Sum Of The Coordinates As 10 Units Studyrankersonline




Draw The Graph Of Each Of The Following Linear Equation In Two Variables X Y 2 Maths Linear Equations In Two Variables Meritnation Com
Graphing and Systems of Equations Packet 3 Graphing Linear Equations Graphing The Linear Equation y = 3x 5 1) Find the slope m = 3 m = 3 = y 1 x 2) Find the yintercept x = 0 , b = 5 (0, 5) 3) Plot the yintercept 4) Use slope to find the next point Start at (0,5) m =Graphing Linear Equations The graph of a linear equation in two variables is a line (that's why they call it linear ) If you know an equation is linear, you can graph it by finding any two solutions ( x 1 , y 1 ) and ( x 2 , y 2 ) ,The linear equations x = 2 and y = − 3 only have one variable in each of them However, because these are linear equations, then they will graph on a coordinate plane just as the linear equations above do Just think of the equation x = 2 as x = 0y 2 and think of y = − 3 as y = 0x – 3




Draw A Graph X Y 4 And X Y 2 Brainly In



Solution Graph The Linear Equation X Y 2
Graphing Linear Equations – Explanation and Examples Graphing linear equations requires using information about lines, including slopes, intercepts, and points, to convert a mathematical or verbal description into a representation of a line in the coordinate plane Though there are many ways to do this, this article will focus on how to use the slopeintercept form to 51 Solving Systems of Linear Equations by Graphing (pp 235–240) Solve the system of linear equations by graphing Question 1 y = 3x 1 y = x – 7 Answer Question 2 y = 4x 3 4x – 2y = 6 Answer Question 3 5x 5y = 15 2x – 2y = 10 Answer 52 Solving Systems of Linear Equations by Substitution (pp 241–246) How do you graph the line #xy=2#?
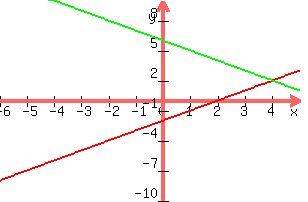



How Do You Solve The System X Y 2 And X Y 6 By Graphing Socratic




Draw A Graph For Linear Equation X Y 2 Brainly In
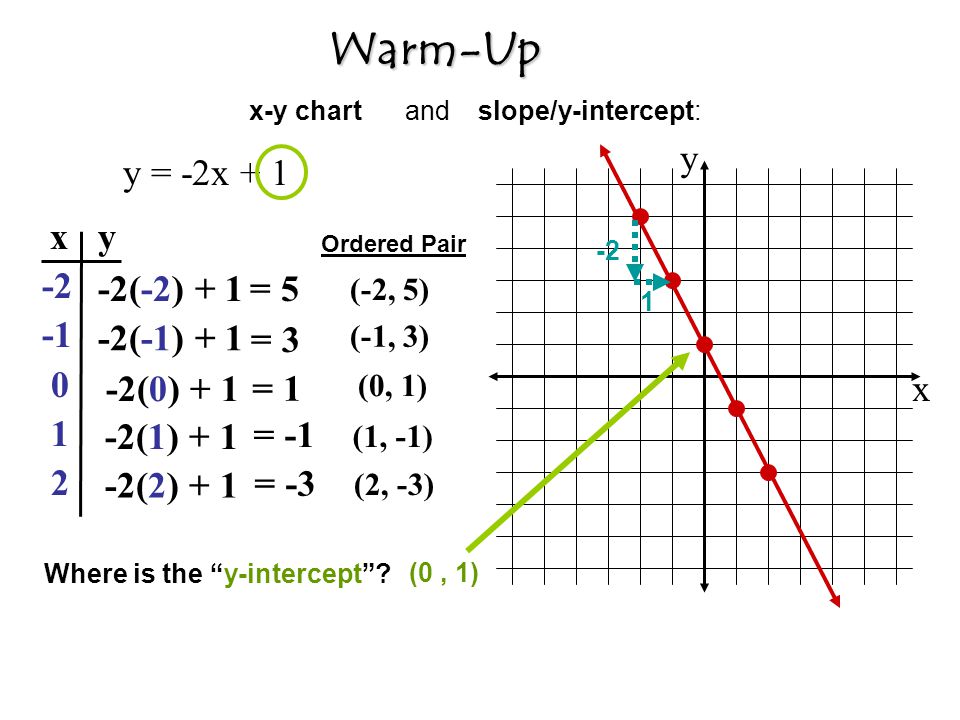



Y 2x 1 X Y Xy 2 1 5 2 0 1 2 1 1 Ordered Pair 2 5 1 3 0 1 1 1 2 3 Where Is The Y Intercept Ppt Download



Objective To Graph Horizontal Vertical And Oblique Lines



Complete The Following Table To Draw Graph Of The Equations I X Y 3 Ii X Y 4 Algebra Shaalaa Com



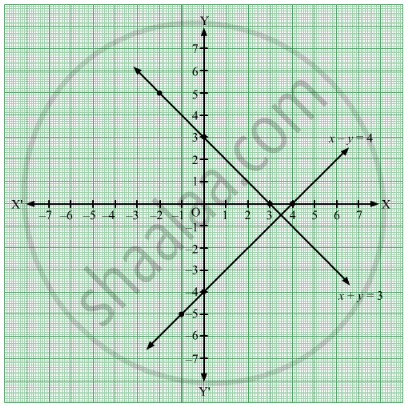
How Do You Solve The System X Y 6 And X Y 2 By Graphing Socratic




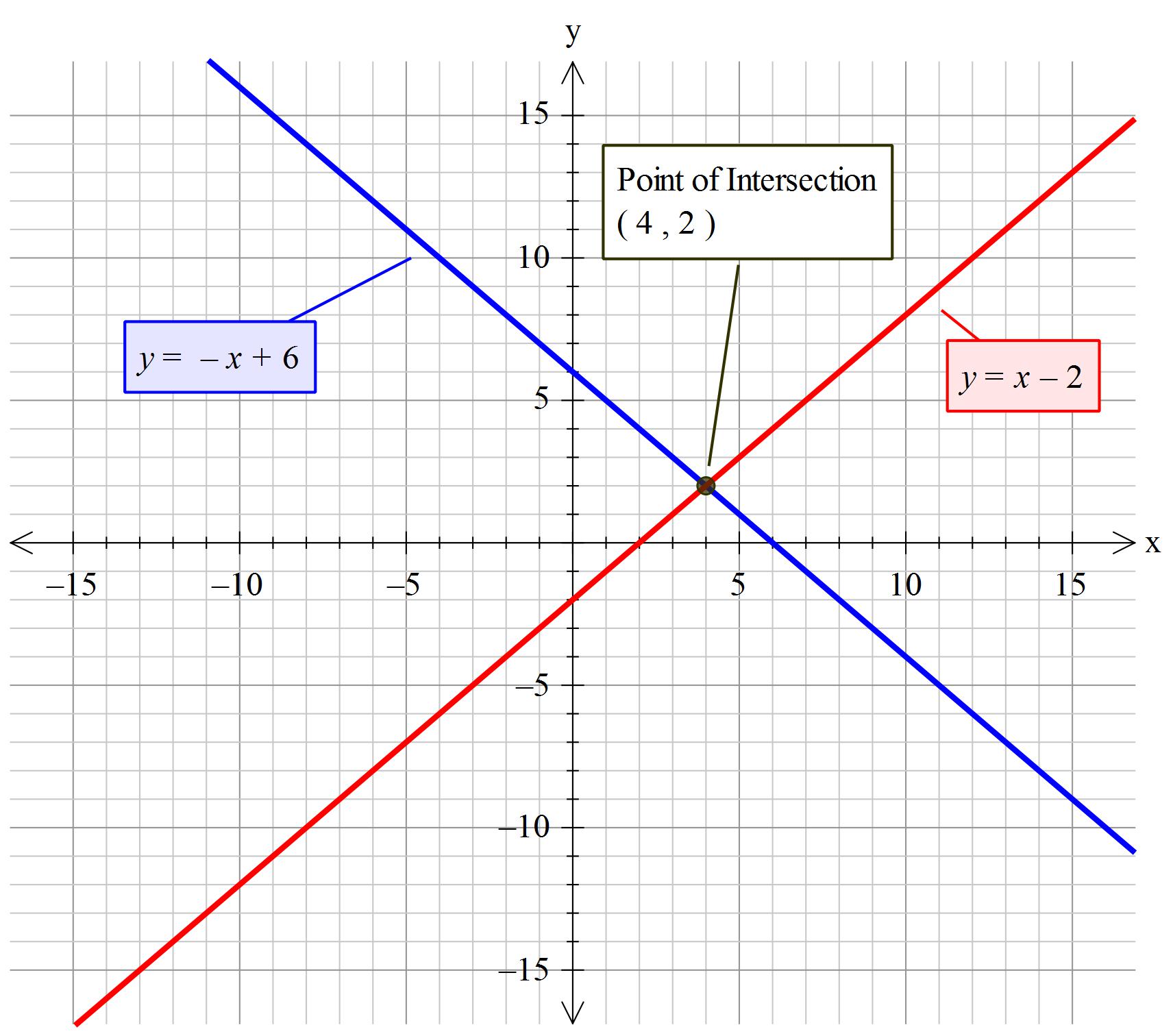
Q3e 3x Y 10 X Y 2 Solve The Following Simultaneous Equation Graphically
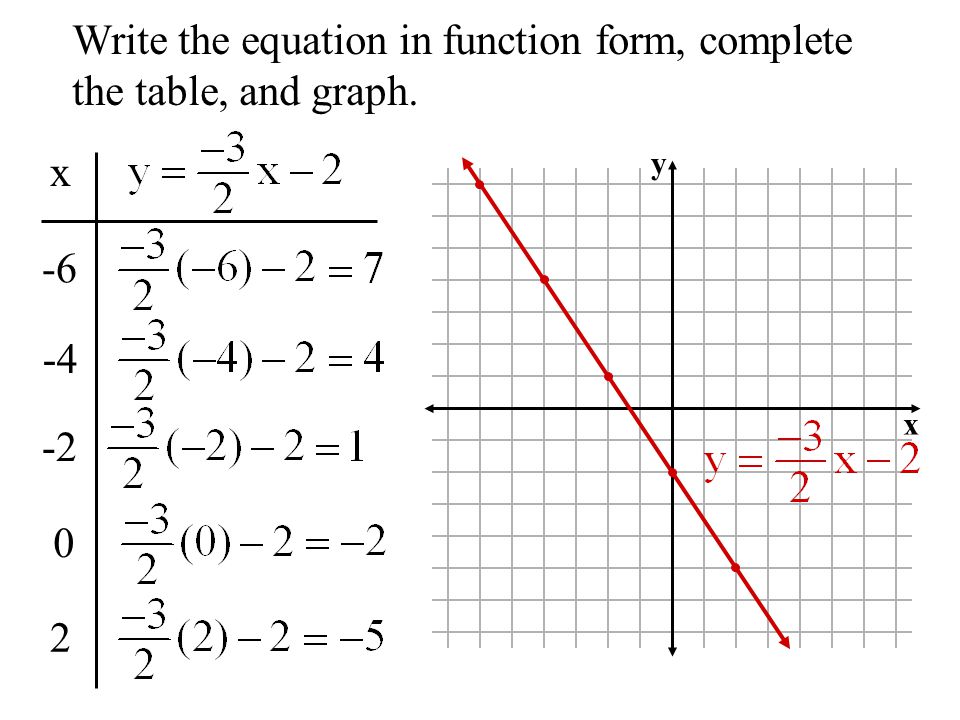



Objective To Graph Horizontal Vertical And Oblique Lines Using Tables Of Values And Intercepts Linear Equations Xy 2x 2 1 3 2 1 Ppt Download
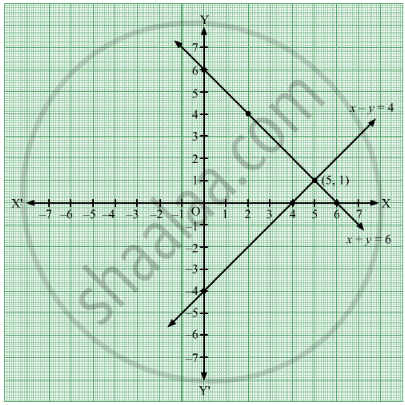



Solve The Following Simultaneous Equations Graphically X Y 6 X Y 4 Algebra Shaalaa Com



Two Variable Linear Equations Intro Video Khan Academy



Graphing Linear Equations What Is A Linear Equation A Linear Equation Is An Equation Whose Graph Is A Line Linear Not Linear Ppt Download
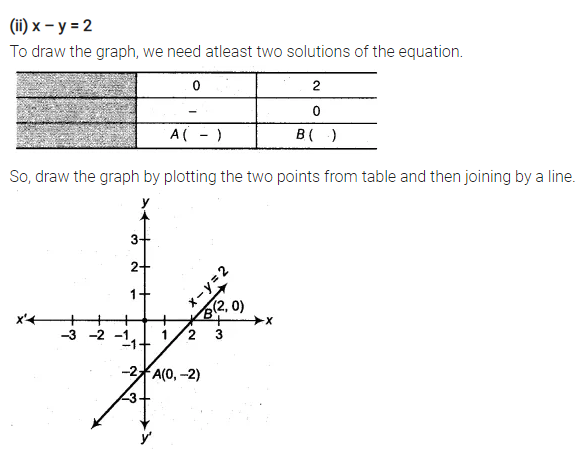



Draw The Graph Of Each Of The Following Linear Equations In Two Variables Cbse Class 9 Maths Learn Cbse Forum




Draw The Graph For Each Of The Equation X Y 6 And X Y 2 On The Same Graph Paper And Find The Coordinates Of The Point Where The Two Straight Lines Intersect




Graphing Inequalities X Y Plane Review Article Khan Academy
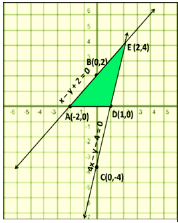



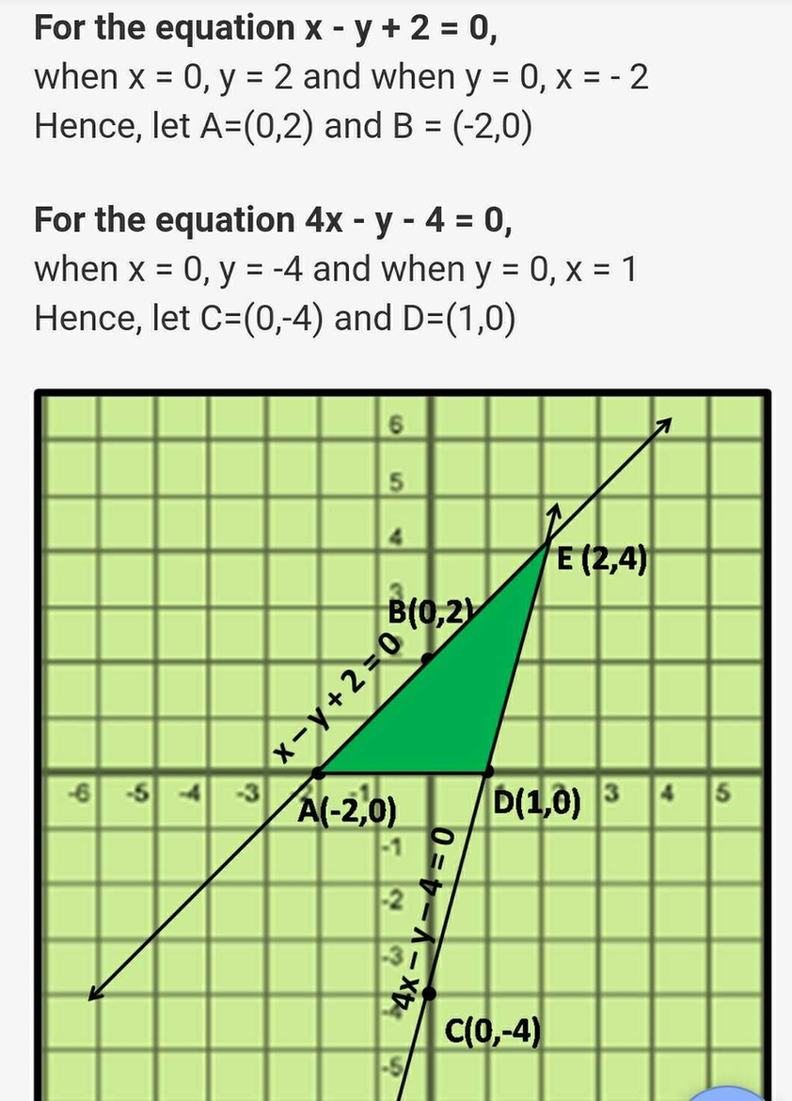
Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 And 4x Y 4 0 Calculate The Area Of The Triangle Formed By The Lines So Drawn And The X Axis Snapsolve




R D Sharma Solutions Class 9th Ch 13 Linear Equations In Two Variables Exercise 13 3



Solution Graph Linear Equation X Y 2 Thanks



What Is The Graph Of Xy 2 Quora
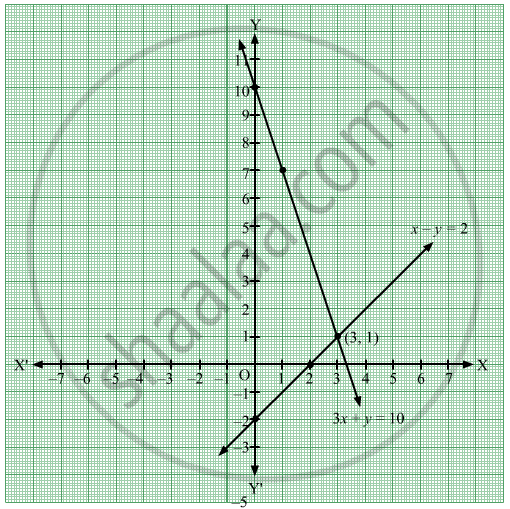



Solve The Following Simultaneous Equation Graphically 3x Y 10 X Y 2 Algebra Shaalaa Com
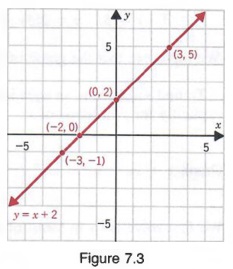



Graph Graph Equations With Step By Step Math Problem Solver
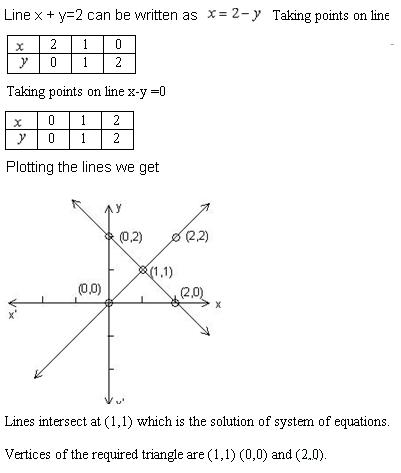



Draw The Graph Of X Y 2 And X Y 0 And Hence Find The Vertices Of The Triangle Formed By The Lines And The X Axis Mathematics Topperlearning Com Sljoqnfee




Draw The Graph Of Linear Equations X Y 4 And X Y 2 On The Same Graph Paper And Find The Coordinates Of Brainly In




Draw The Graph For Each Of The Equation X Y 6 And X Y 2 On The Graph And Find The Coordinates Of The Maths Linear Equations In Two Variables Meritnation Com




Draw The Graph Of Each Of The Following Linear Equations In Two Variables X Y 4 X Y 2 Y 3x 3 2x Y Youtube




3



Solution X Y 10 X Y 2




5 1 Equations Of Lines Equations Of The Form Ax By C Are Called Linear Equations In Two Variables X Y 2 2 This Is The Graph Of The Equation 2x Ppt Video Online Download



Solution Graph Solution Set Of This Linear Inequality X Y Gt 2



Ove The Toliowing Pair Or Linear Equathos D 4x Y 4 0 Q 4 D Scholr




Q Draw The Graph Of 2 Lines Where Equation Are X Y 6 0 And X Y 2 0 On The Same Graph Paper Maths Linear Equations In Two Variables Meritnation Com




Draw The Graph Of The Linear Equations In Two Variable X Y 2 Brainly In



How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic



File Y Equals X Plus 2 Png Wikimedia Commons



Draw The Graph Of Each Of The Following Linear Equations In Two Variables I X Y 4 Ii X Y 2 Youtube



1




How To Graph Linear Equations 5 Steps With Pictures Wikihow



Ay 10 Graph The Linear Equation X Y 2 Use The Chegg Com




52 Draw The Graph Of The Pair Of Linear Equations X Y 2 0 And 4 X Y 4 0 Calculate The Area Of The Triangle Formed By The Lines So Drawn And The X Axis




Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12
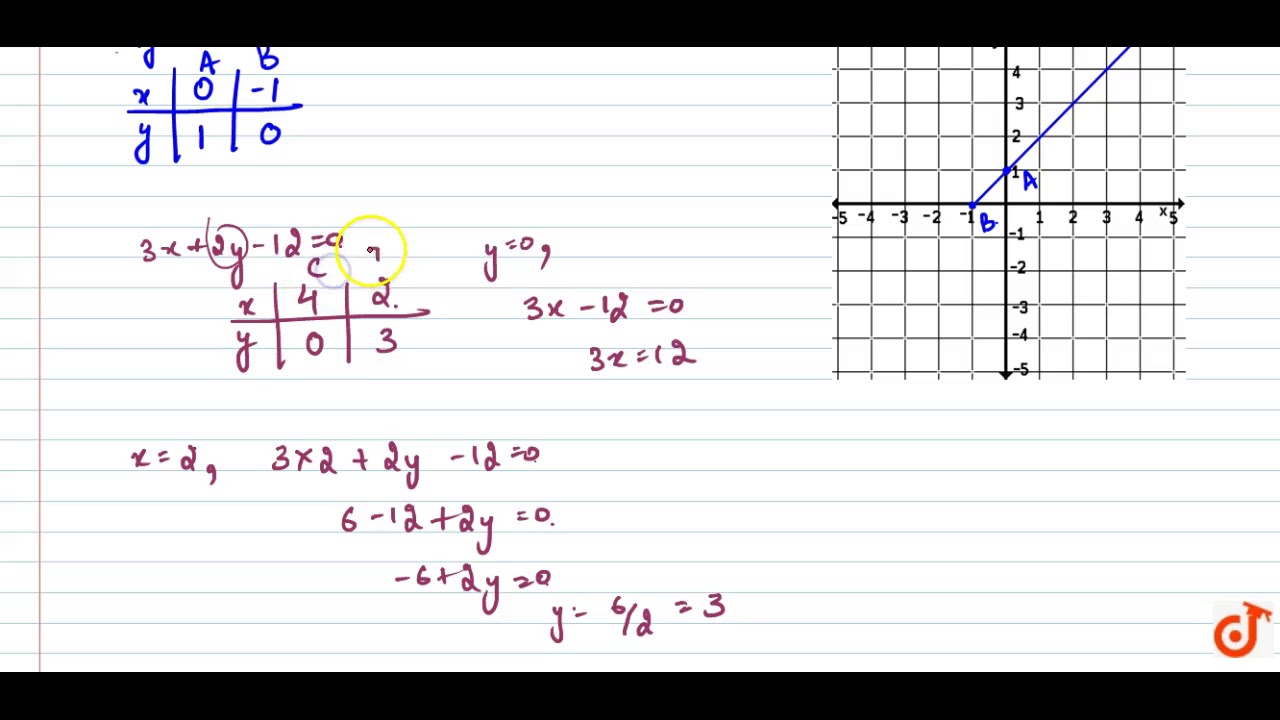



Draw The Graphs Of The Equations X Y 1 0 And 3x 2y 12 0 Determine The Coordinates Of The V Youtube




Draw The Graph Of Pair Of Linear Equations X Y 2 0 And 4x Y 4 0 Calculate The Area Of Triangle Brainly In
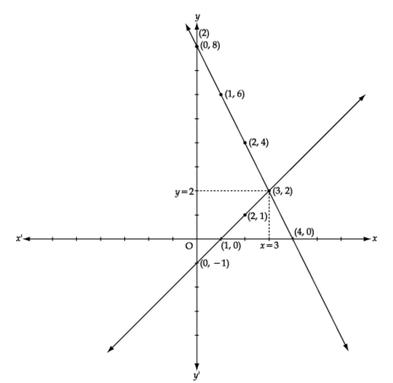



Solve X Y 1 And 2x Y 8 Graph Mathematics Topperlearning Com 4q3fx13uu
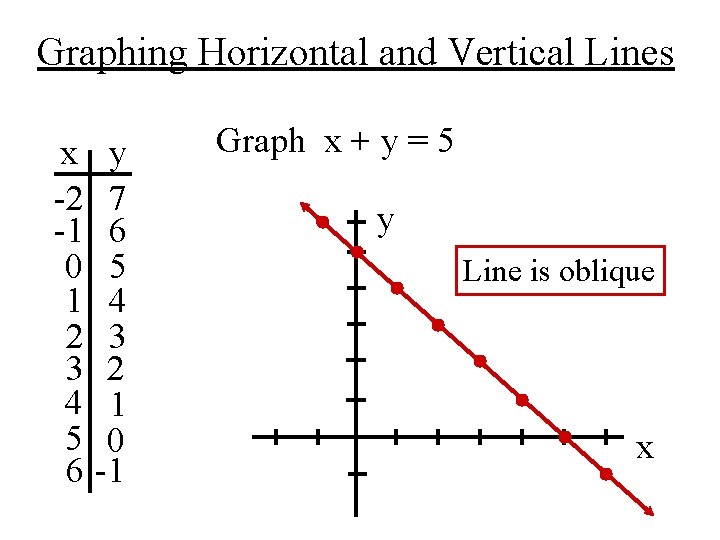



Objective To Graph Horizontal Vertical And Oblique Lines




Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 Amp 4x Y 4 0 Determine The Co Ordinates Of The Vertices Of The Triangle Formed By The Lines




Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12 0
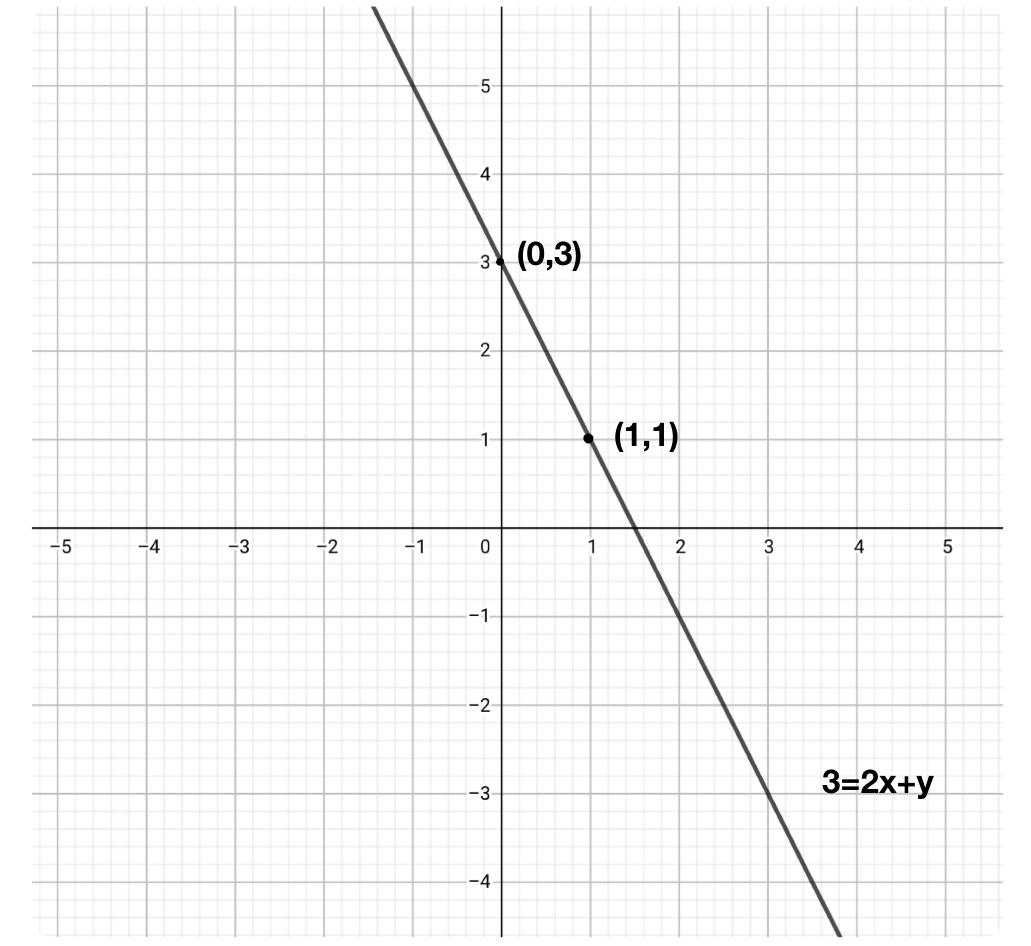



Draw The Graph Of Each Of The Following Linear Equations Class 9 Maths Cbse
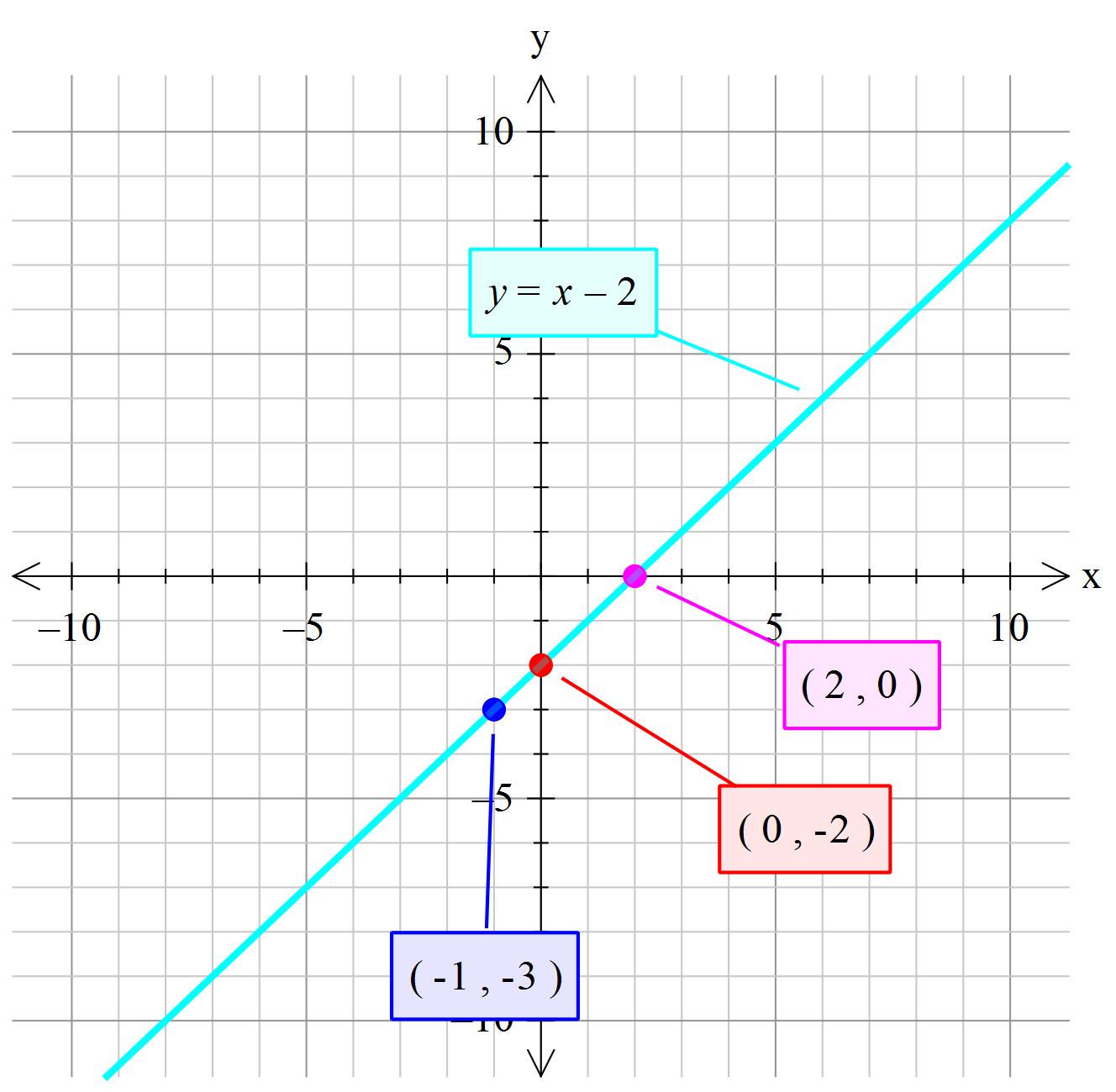



How Do You Graph The Line X Y 2 Socratic




Solve The Equation Graphically X Y 4 And X Y 2 And Verify The Answer By Using Consisitency Maths Pair Of Linear Equations In Two Variables Meritnation Com




Ex 4 3 1 Iv Draw Graph Of Linear Equation 3 2x Y Video




X Y 2 Graph The Linear Equation Chavachel



What Is The Graph Of Xy 2 Quora



Let S Draw Graphs Of X Y 4 2x Y 2 And Observe Them Sarthaks Econnect Largest Online Education Community
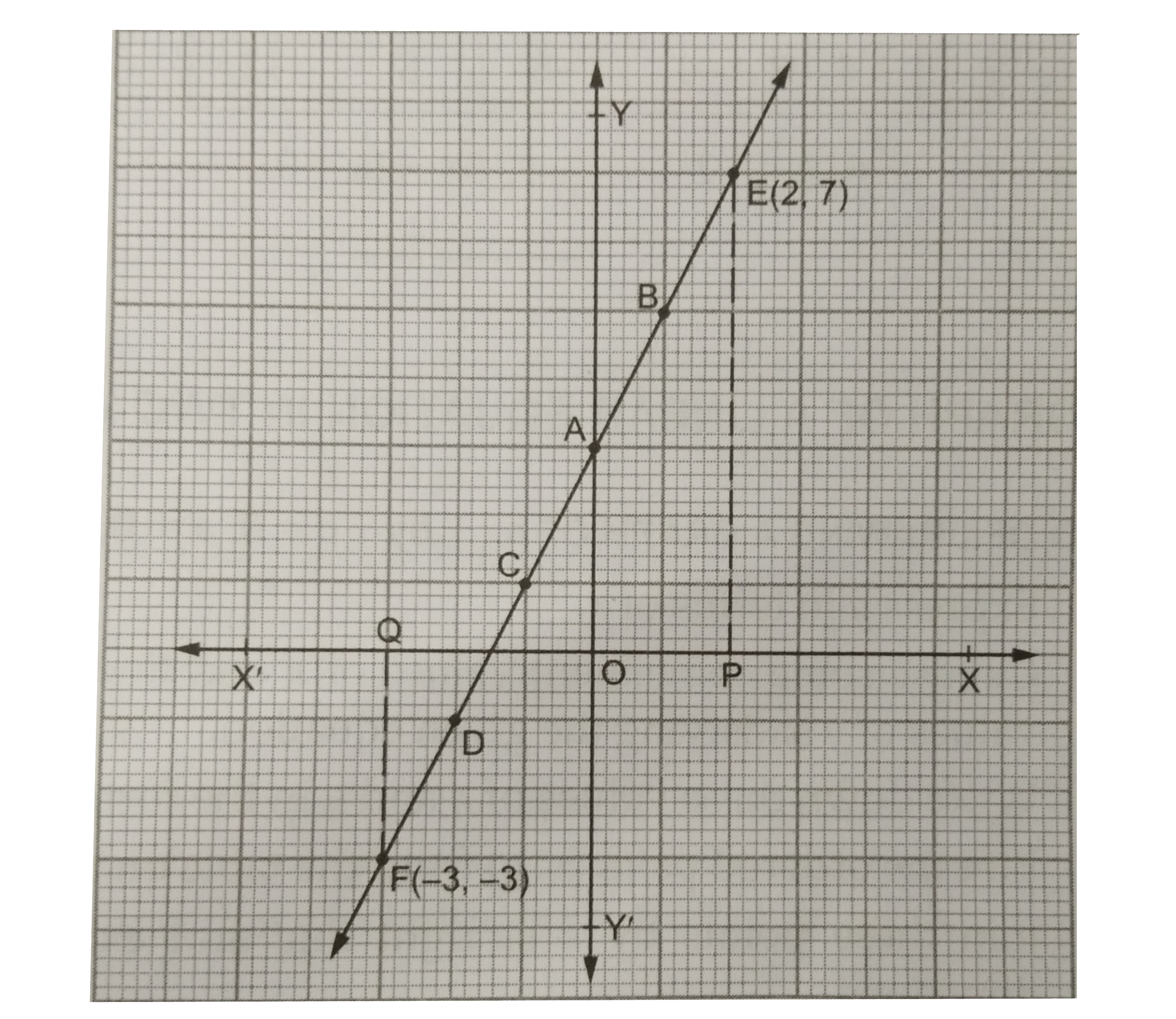



Draw The Graph Of The Equation 2x Y 3 0 Using The Graph Find The Value Of Y When A X 2 B X 3
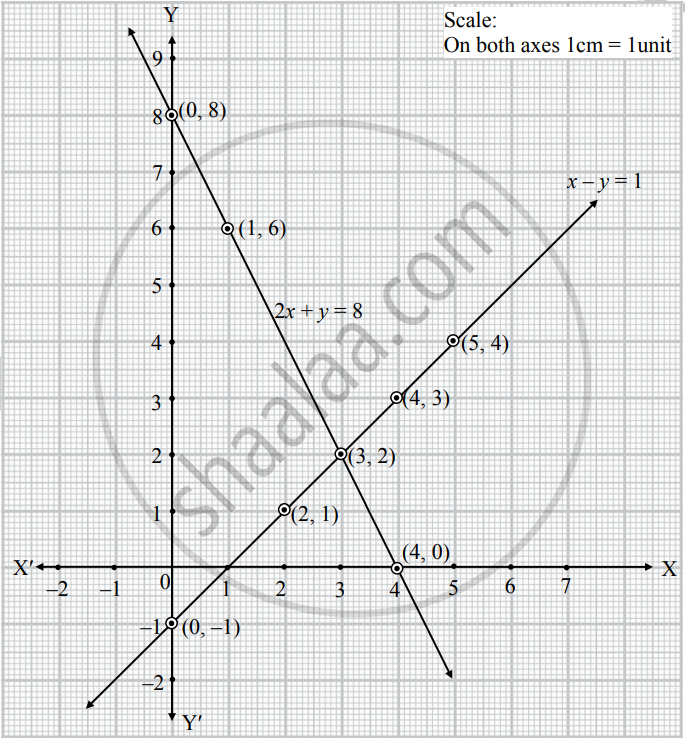



Solve The Following Equations By Graphical Method X Y 1 2x Y 8 Algebra Shaalaa Com



Solution Solve By Graphing X Y 2 X Y 6
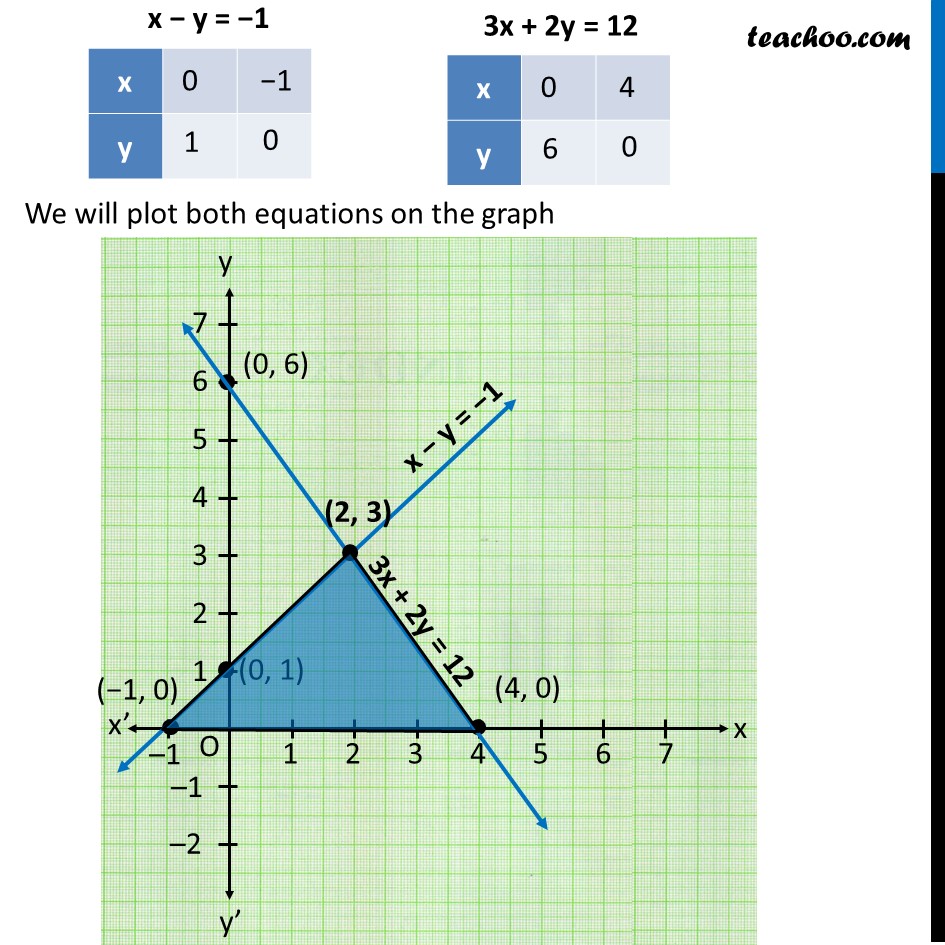



Ex 3 2 7 Draw Graphs Of X Y 1 0 And 3x 2y 12 0
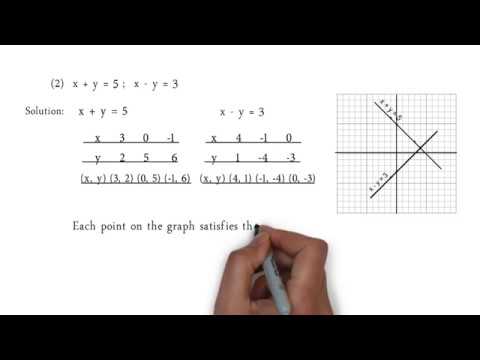



X Y 5 And X Y 3 P S 1 2 Q2 2 Linear Equations In Two Variables Youtube




Draw The Graph Of The Following Linear Equation In Two Variables X Y 2



What Is The Graph Of Xy 2 Quora




Draw The Graph Of X Y 6 X Y 2 On The Same Graph And Find The Co Ordinates Of The Point Where Maths Linear Equations In Two Variables Meritnation Com




Draw The Graph Of Each Of The Following Linear Equation In Two Variables Ii X Y 2 Brainly In



Draw The Graphs Of The Equations X Y 10 0 And X Y 4 0 On The Same Graph Paper Mathematics Topperlearning Com V7mfc1zxx



Solution Can You Assist Me To Solved This Linear Equation By Graphing X 2y 5 X Y 2 How Do I Determin Wheather The Following Has One Solution No Solution Or Many Solution Y X 2




Ex 4 3 1 I Draw The Graph Of Linear Equation X Y 4 Teachoo



How Do You Solve The System Of Equations X Y 8 X Y 4 By Graphing Socratic




Ex 6 2 5 Solve X Y 2 Graphically Chapter 6 Cbse
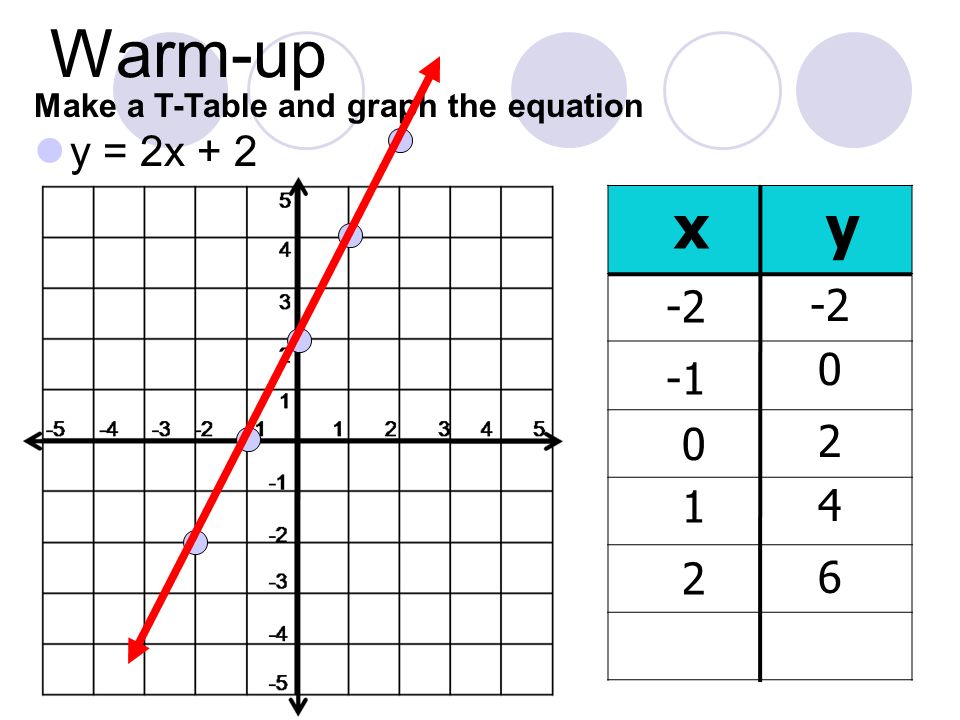



Warm Up Make A T Table And Graph The Equation Y 2x 2 X Y Ppt Video Online Download




Draw The Graph Of X Y 2 Please I Need Answer Brainly In



1
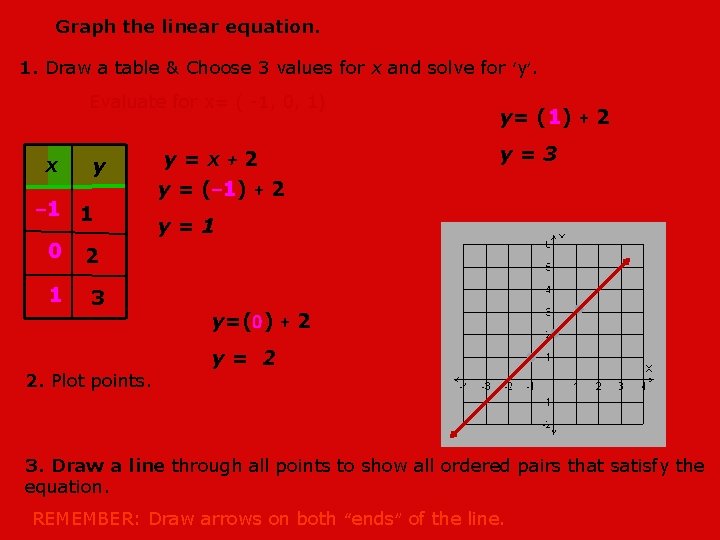



Graph The Linear Equation Yx 2 1 Draw




Draw The Graphs Of The Lines X Y 1 And 2x Y 8 Shaded The Areas Formed By These Two Lines And The Y Axis Also Find This Area



Solution Directions Solve Each System Of Linear Equations By Graphing Problem X Y 4 X Y 2 I Have No Idea What To Do Here
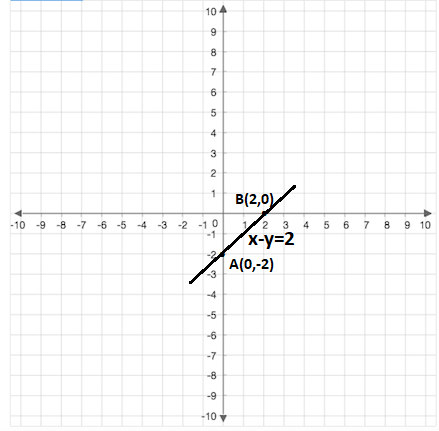



Draw The Graph For The Linear Equation X Y 2 In Two Variables Snapsolve




Solved Graph The Linear Equation By Finding And Plotting Its Chegg Com




Ask Questions For Cbse Class 9 Maths Linear Equations In 2 Variables
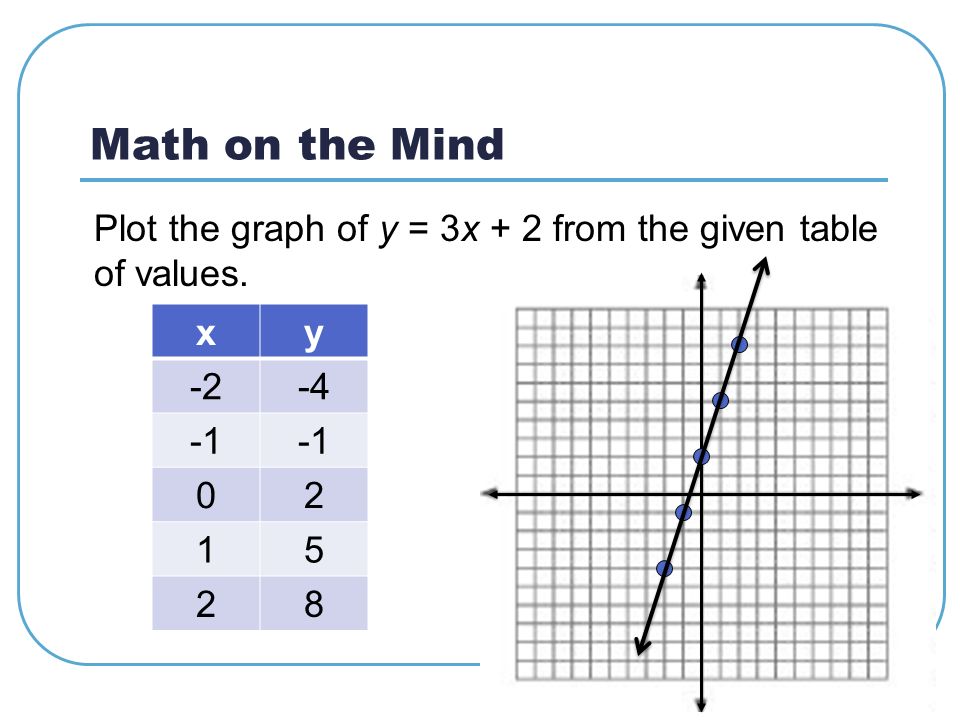



Math On The Mind Plot The Graph Of Y 3x 2 From The Given Table Of Values Xy Ppt Download
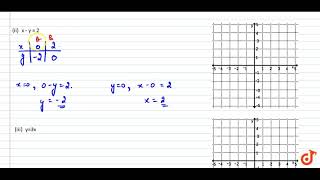



Draw The Graph Of Each Of The Following Linear Equations In Two Variables I X Y 4 Ii X Y Youtube
1685927.png)



Draw The Graph Of Each Of The Following Linear Equation In Two Variables Y 3x 3 2x Y X Y 2 Maths Linear Equations In Two Variables Meritnation Com




Part 4 Class 9 Maths Linear Equation In 2 Variables Ncert Solutions Ex 4 3 Youtube



Solve The Following Systems Of Equations Graphically X Y 6 X Y 2 Sarthaks Econnect Largest Online Education Community




Draw A Graph Of Equation 2x Y 6 And X Y 2 And Find The Area Of Triangle So Formed Maths Linear Equations In Two Variables Meritnation Com
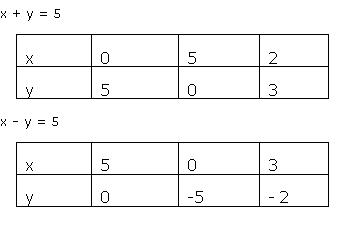



Draw The Graphs Of The Following Equations X Y 5 X Y 5 I Find The Solution Of The Equations From The Graph Ii Shade The Triangular Region Formed By Th Mathematics Topperlearning Com Rmtc0aktt




Example 6 Draw The Graph Of X Y 7 Chapter 4 Examples




Draw The Graph Of Two Lines Whose Equations Are X Y 6 0 And X Y 2 0 On The Sample Graph Paper Find The Brainly In


